The Monad Laws: Verifying the Kleisli Composition Monoid
Having explored Functors and the crucial concept of structure preservation, we now turn our attention to Monads. Monads represent another fundamental structure in functional programming, often used to sequence computations that involve some form of context, such as handling potential absence of values (Option), managing multiple possible outcomes (List), dealing with asynchronous operations (Async, Task), or managing state.
To ensure these sequenced computations behave predictably and compose reliably, the core operations provided by a Monad must adhere to specific rules: the Monad Laws. This chapter aims to illuminate these laws, providing a deeper understanding of what makes a Monad work.
Recap: Kleisli Arrows
Section titled “Recap: Kleisli Arrows”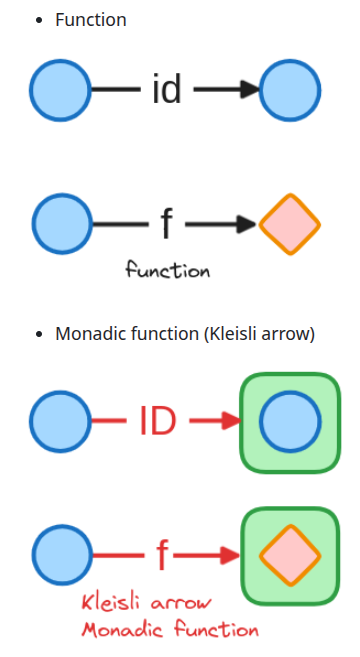
First, let’s recall Kleisli arrows from Unit 2, Section 5. These are the specialized functions that Monads are designed to work with. Unlike regular functions ('a -> 'b), Kleisli arrows take a regular value ('a) and return a value wrapped in the monadic context M ('a -> M<'b>). They represent a computation step whose result is context-dependent.
The bind Operation
Section titled “The bind Operation”The primary mechanism Monads provide for sequencing Kleisli arrows is the bind operation. Often represented by the infix operator >>=, bind allows us to chain computations where the next step (a Kleisli arrow) depends on the result produced within the monadic context by the previous step.
Its signature, using the pipeline style we favor, is:
bind : ('a -> M<'b>) -> M<'a> -> M<'b>
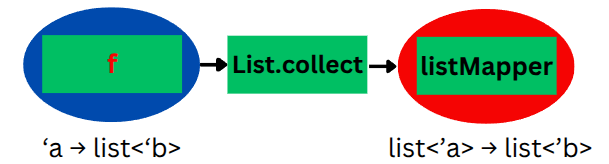
List Monad is list.collect in F#
Section titled “List Monad is list.collect in F#”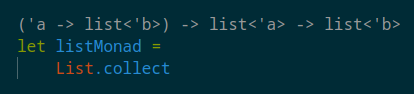
Or, written infix:
(>>=) : M<'a> -> ('a -> M<'b>) -> M<'b>
Usage looks like: monadicValueA |> bind kleisliArrowF. This takes the result(s) from monadicValueA, feeds them into kleisliArrowF, and returns the resulting M<'b>.
Understanding the Monad Laws: The Kleisli Monoid Approach
Section titled “Understanding the Monad Laws: The Kleisli Monoid Approach”How do we ensure that chaining operations with bind is well-behaved? This is where the Monad Laws come in. Typically, three laws involving bind and an identity operation (which we’ll call ID) are presented.
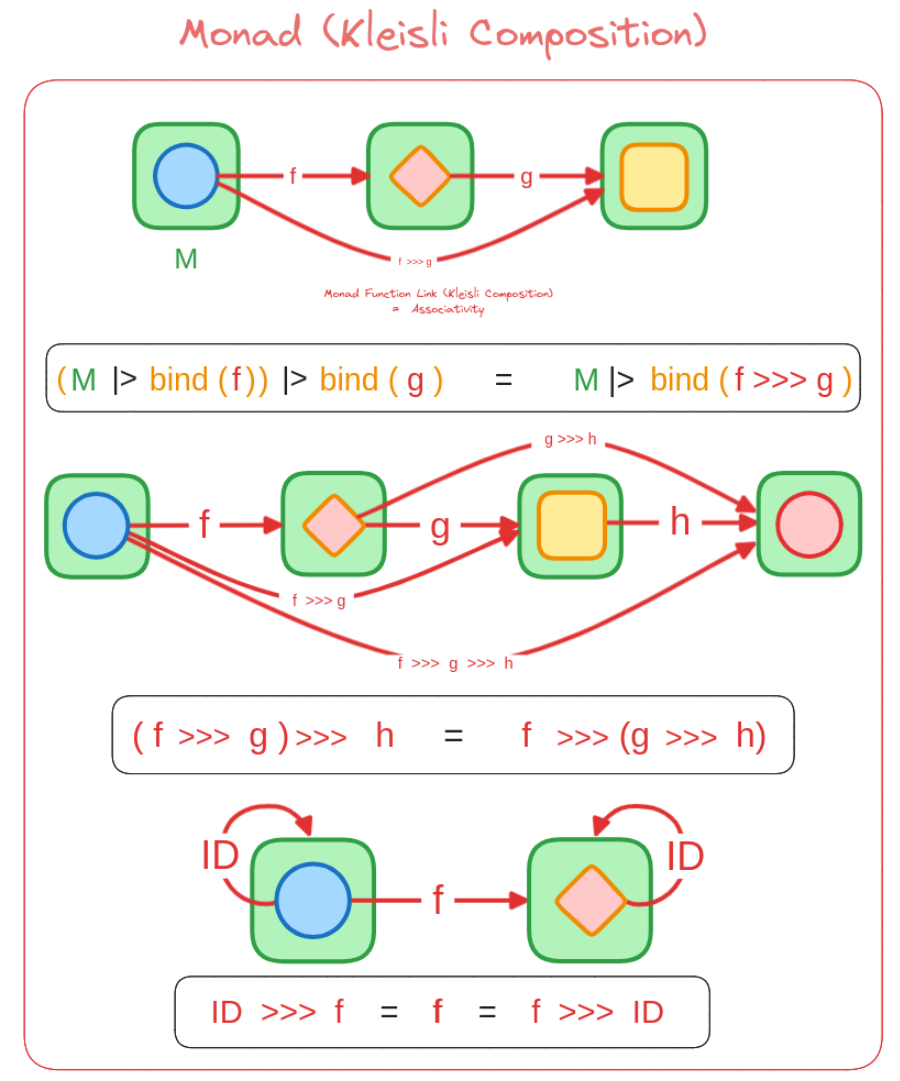
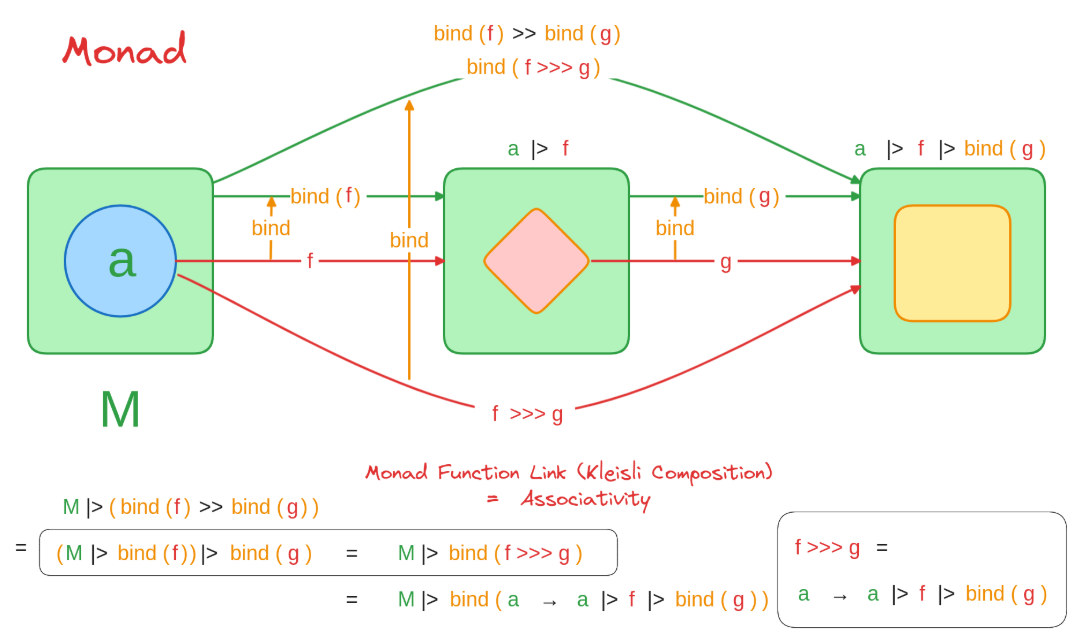
However, there’s an equivalent formulation that arguably provides deeper insight into the algebraic structure Monads impose. This approach focuses on defining composition directly for Kleisli arrows. Let’s denote this Kleisli composition operator as >>>.
A type constructor M forms a Monad if and only if its Kleisli arrows ('a -> M<'b>) form a Monoid under this composition operator >>>, with the identity Kleisli arrow (ID : 'a -> M<'a>) acting as the Monoid’s identity element.
Why adopt this perspective? Because it connects directly to concepts we’ve already established:
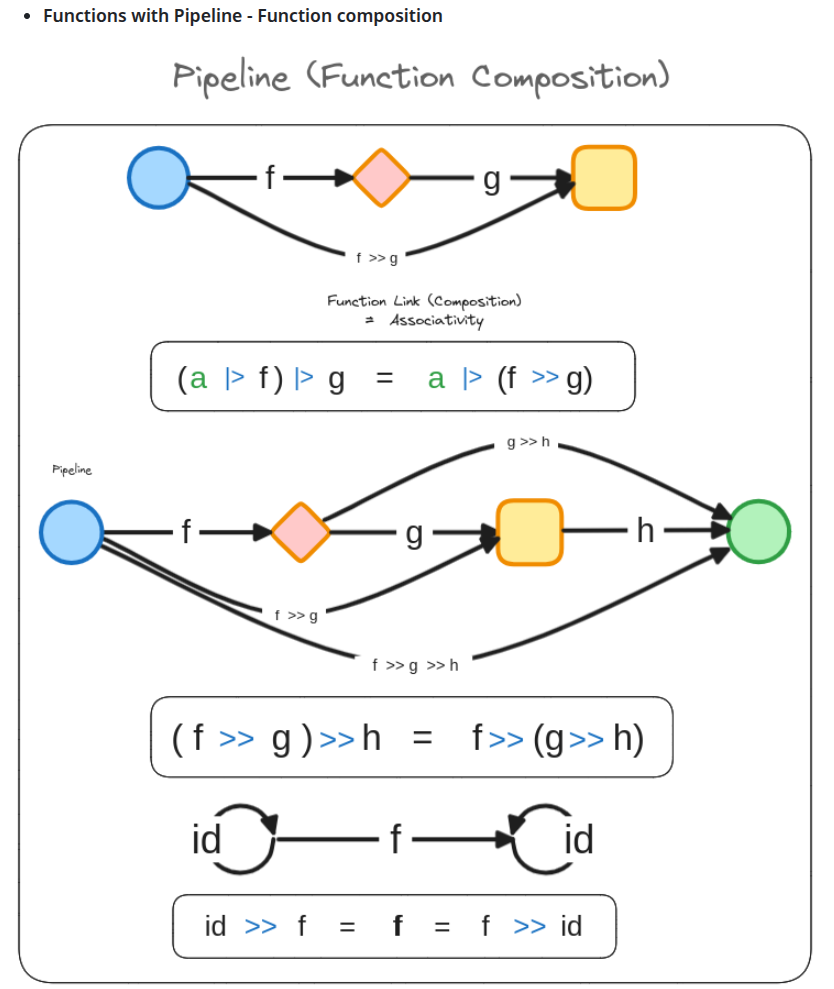
- We know function composition (
>>) forms a natural Monoid (associativity +id). - We established that preserving this compositional structure is key for robust abstractions like Functors.
The Kleisli Monoid approach reveals that Monads achieve robustness by ensuring that the composition of Kleisli arrows (>>>) also adheres to the fundamental Monoid laws (associativity and identity laws) using ID as the identity. The standard Monad laws for bind are precisely the conditions needed to guarantee this Kleisli Monoid structure holds.
Therefore, in this chapter, we will verify the Monad structure by demonstrating these Kleisli Monoid properties, highlighting the core algebraic foundation.
Definitions for General Monad M
Section titled “Definitions for General Monad M”Let M represent any type constructor that forms a valid Monad.
- Kleisli Arrow (Monadic Function): A function with the signature:
'a -> M<'b> - Identity Kleisli Arrow (
ID): The function that lifts a plain valueainto the minimal monadic contextM.val ID<'a> : 'a -> M<'a> - Kleisli Composition (
>>>): An operator to compose two Kleisli arrows, defined usingbind.val inline (>>>) : ('a -> M<'b>) -> ('b -> M<'c>) -> ('a -> M<'c>)The definition is:let (>>>) f g = fun a -> (f a) |> bind g(Read as: Apply Kleisli arrowftoa, yielding anM<'b>, then pipe this result intobindwith the next Kleisli arrowg.)
Setup for Examples (Generic)
Section titled “Setup for Examples (Generic)”Let’s define some generic Kleisli arrows for illustration, assuming M is a valid Monad providing M.ID and a bind function.
// Assume M is a valid Monad with M.ID and bind defined.
// Sample Kleisli Arrowslet f: int -> M<string> = fun i -> M.ID (sprintf "f(%d)" i)let g: string -> M<float> = fun s -> M.ID (float s.Length)let h: float -> M<bool> = fun fl -> M.ID (fl > 10.0) // Example: check if float > 10.0
// Initial Monadic Valuelet initialValue = 5let initialMonadValue : M<int> = M.ID initialValueVerification of Kleisli Monoid Laws (via Standard Monad Laws)
Section titled “Verification of Kleisli Monoid Laws (via Standard Monad Laws)”We now demonstrate that if M is a valid Monad (meaning bind and ID satisfy the standard Monad laws), then the Kleisli composition >>> (defined via bind) necessarily satisfies the Monoid laws with ID.
Law 1: Associativity
Section titled “Law 1: Associativity”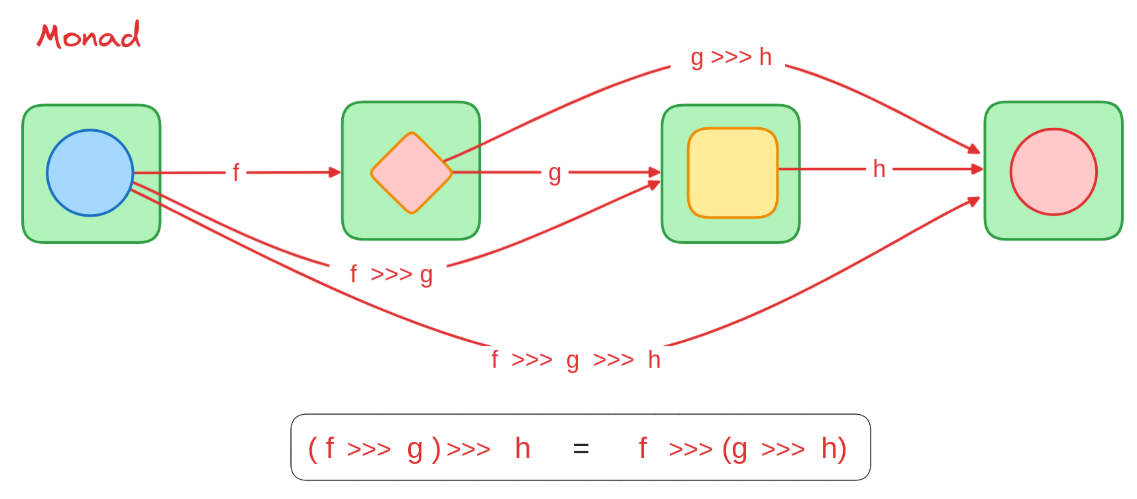
- Equation:
(f >>> g) >>> h = f >>> (g >>> h) - Goal: Show that composing Kleisli arrows
f,g, andhis associative. This means applying the differently grouped compositions to an initial valueashould yield identical results in the contextM. - Illustrative Code Structure (Conceptual):
// Let's apply both sides to an initial value 'a'// --- LHS applied to 'a' ---// ( (f >>> g) >>> h ) a// = ( fun intermediate_value -> ((f >>> g) intermediate_value) |> bind h ) a // Definition of >>>// = ( (fun input_f -> (f input_f) |> bind g) >>> h ) a// = ( (f a) |> bind g ) |> bind h // Applying definitions// --- RHS applied to 'a' ---// ( f >>> (g >>> h) ) a// = ( fun intermediate_value -> (f intermediate_value) |> bind (g >>> h) ) a // Definition of >>>// = (f a) |> bind (fun x -> (g x) |> bind h) // Applying definitions// We need to show:// ( (f a) |> bind g ) |> bind h IS EQUIVALENT TO (f a) |> bind (fun x -> (g x) |> bind h)// Let m = f a. We need to show:// ( m |> bind g ) |> bind h IS EQUIVALENT TO m |> bind (fun x -> g x |> bind h)
- Equivalence Explanation: The required equivalence,
(m |> bind g) |> bind h = m |> bind (fun x -> g x |> bind h), is precisely the associativity law of thebindoperation itself (one of the three standard Monad laws). By definition, forMto be a Monad, itsbindoperation must be associative. This associativity ofbinddirectly guarantees the associativity of the Kleisli composition>>>derived from it. Therefore, the Associativity Law holds for>>>(guaranteed bybind’s associativity).
Law 2: Left Identity
Section titled “Law 2: Left Identity”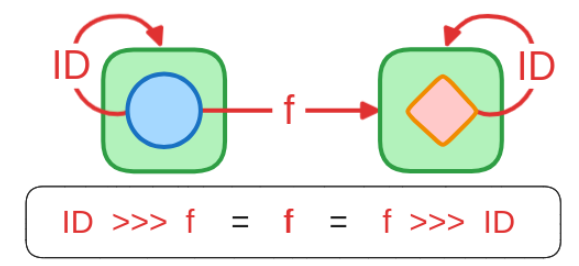
- Equation:
ID >>> f = f - Goal: Show that composing the identity Kleisli arrow
IDbeforefhas no effect; the result is equivalent tofitself. - Illustrative Code Structure (Conceptual):
// Let's apply both sides to an initial value 'a'// --- LHS applied to 'a' ---// ( ID >>> f ) a// = ( fun intermediate_value -> (ID intermediate_value) |> bind f ) a // Definition of >>>// = ( ID a ) |> bind f // Applying definitions// --- RHS applied to 'a' ---// f a// We need to show:// ( ID a ) |> bind f IS EQUIVALENT TO f a
- Equivalence Explanation: The required equivalence,
(ID a) |> bind f = f a, is precisely the left identity law for thebindoperation (another standard Monad law). By definition, forMto be a Monad, itsbindandIDoperations must satisfy this law. This directly guarantees thatIDacts as the left identity for the derived Kleisli composition>>>. Therefore, the Left Identity Law holds for>>>(guaranteed bybind’s left identity).
Law 3: Right Identity
Section titled “Law 3: Right Identity”
- Equation:
f >>> ID = f - Goal: Show that composing
fwith the identity Kleisli arrowIDafterwards has no effect; the result is equivalent tofitself. - Illustrative Code Structure (Conceptual):
// Let's apply both sides to an initial value 'a'// --- LHS applied to 'a' ---// ( f >>> ID ) a// = ( fun intermediate_value -> (f intermediate_value) |> bind ID ) a // Definition of >>>// = ( f a ) |> bind ID // Applying definitions// --- RHS applied to 'a' ---// f a// We need to show:// ( f a ) |> bind ID IS EQUIVALENT TO f a// Let m = f a. We need to show:// m |> bind ID IS EQUIVALENT TO m
- Equivalence Explanation: The required equivalence,
m |> bind ID = m, is precisely the right identity law for thebindoperation (the third standard Monad law). By definition, forMto be a Monad, itsbindandIDoperations must satisfy this law. This directly guarantees thatIDacts as the right identity for the derived Kleisli composition>>>. Therefore, the Right Identity Law holds for>>>(guaranteed bybind’s right identity).
Conclusion
Section titled “Conclusion”We have demonstrated that the standard Monad Laws, typically expressed in terms of bind and ID, are mathematically equivalent to requiring that Kleisli composition (>>>) forms a Monoid with ID as its identity element.

If a type constructor M along with its ID and bind operations satisfy the three standard Monad laws (left identity, right identity, associativity of bind), then its associated Kleisli composition >>> is guaranteed to be associative and have ID as its identity.
This Kleisli Monoid perspective reinforces the idea that Monads are fundamentally about providing a structured, predictable way to compose computations within a context. The laws ensure that this composition mechanism adheres to the robust algebraic properties of a Monoid, fulfilling the “structure preservation” goal we discussed earlier and enabling the reliable chaining of monadic operations.