Product or Pointwize(ZIP)
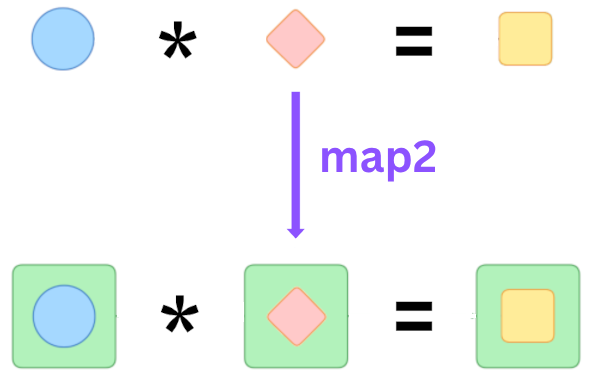
map2 is about binary operations of containers, which makes it fundamentally different from Functor’s map function or Monad’s bind function, leading to a wide variety of implementation methods.
map2: ('a -> 'b -> 'c) -> F<'a> -> F<'b> -> F<'c>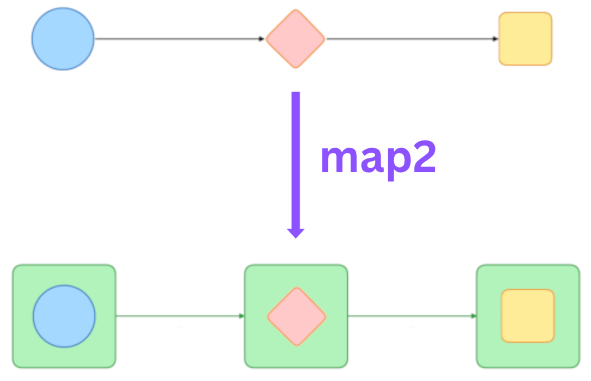
First Branch: Classification by Dependency
Section titled “First Branch: Classification by Dependency”All map2 implementations can be broadly classified into two major categories based on computational dependency:
- Independent / Parallelizable: The two containers are independent of each other
- Dependent / Sequential Processing Required: The result of one computation affects the other
Second Branch: Internal Classification of Independent Systems
Section titled “Second Branch: Internal Classification of Independent Systems”Systems capable of independent and parallel processing can be further subdivided into two categories:
- Cartesian Product
- Pointwise (or ZIP)
1. Cartesian Product Pattern - The “Multiplication Table” Approach
Section titled “1. Cartesian Product Pattern - The “Multiplication Table” Approach”A Cartesian Product generates every possible combination between elements of two collections. It’s easy to understand if you imagine a basic multiplication table from elementary school:
× | 1 2 3--|--------1 | 1 2 32 | 2 4 63 | 3 6 9Here, each cell in the table represents a unique combination (e.g., 2 from the first row and 3 from the first column combine to make 6). The key is that the result for each cell is independent of the others.
Why is this great for parallel processing? Since each combination can be processed on its own, without needing information from any other combination, you can easily split the work among many processors or computers. This makes it highly efficient for tasks that involve exploring every possible combination, like trying out all possible settings in an experiment or generating all unique pairs from two different lists of data.
F# List Implementation Example
Section titled “F# List Implementation Example”let cartesianMap2 f list1 list2 = [for x in list1 do for y in list2 do yield f x y]
let list1 = [1; 2; 3]let list2 = [10; 20; 30]let result = cartesianMap2 (+) list1 list2// result: [11; 21; 31; 12; 22; 32; 13; 23; 33]// (1+10), (1+20), (1+30), // x=1 with all y's// (2+10), (2+20), (2+30), // x=2 with all y's// (3+10), (3+20), (3+30) // x=3 with all y's2. Pointwise (or ZIP) Pattern - The “Parallel Matching” Approach
Section titled “2. Pointwise (or ZIP) Pattern - The “Parallel Matching” Approach”Imagine you have two lists, like a list of students and a separate list of their test scores. A Pointwise operation, often called ZIP, works by combining items that are at the same position in each list. It’s like zipping up two zippers, matching teeth that align perfectly.
For example, if you have:
- Students: [Alice, Bob, Carol]
- Scores: [90, 85, 92]
A Pointwise (ZIP) operation would combine them like this:
- (Alice, 90)
- (Bob, 85)
- (Carol, 92)
Notice that Alice is only matched with 90, not 85 or 92. The resulting collection will have the same number of items as the shortest input list.
Why is this excellent for parallel processing? Just like with the Cartesian Product, each pair (or group of matched items) can be processed completely independently. This means you can easily distribute the task of combining or operating on these matched pairs across multiple processors. Pointwise operations are common when you need to perform an action on corresponding elements from several datasets, such as adding two matrices element by element, or applying a function to pairs of values that are already naturally aligned.
F# List Implementation Example (Pointwise/ZIP)
Section titled “F# List Implementation Example (Pointwise/ZIP)”let pointwiseMap2 f list1 list2 = // Create indexed pairs for both lists let indexedList1 = List.mapi (fun i x -> (i, x)) list1 let indexedList2 = List.mapi (fun i x -> (i, x)) list2
// Perform a Cartesian-like loop on the indexed lists, // then filter to keep only elements with matching indices. // This mimics List.map2 behavior without using List.map2 directly. let result = [ for (i1, x) in indexedList1 do for (i2, y) in indexedList2 do if i1 = i2 then // Only process if indices match yield f x y ] result
let list3 = [1; 2]let list4 = [10; 20; 30]let result2 = pointwiseMap2 (+) list3 list4// result2: [11; 22]// (1+10), (2+20) - Processes up to the length of the shorter listF# built-in List.map2 (Pointwise/ZIP)
Section titled “F# built-in List.map2 (Pointwise/ZIP)”Actually, F# has the built-in map2 in List name space, and it works in the pointwise/ZIP way.
let list1 = [1; 2; 3]let list2 = [10; 20; 30]
// Apply the addition function (+) pointwise to list1 and list2let result = List.map2 (+) list1 list2// result: [11; 22; 33]// (1+10), (2+20), (3+30)// Each element from list1 is combined with the element at the same position in list2.This F# code snippet demonstrates a pointwise operation using List.map2.
List.map2 is a built-in F# function that applies a given function (in this case, addition (+)) to corresponding elements from two lists. It processes the lists in parallel, taking the first element from list1 and the first from list2, then the second from list1 and the second from list2, and so on.
For our example:
1fromlist1is added to10fromlist2, resulting in11.2fromlist1is added to20fromlist2, resulting in22.3fromlist1is added to30fromlist2, resulting in33.
Therefore, result will be [11; 22; 33]. This operation combines each element from list1 with the element at the same position in list2.
What if lists have different lengths?
let list3 = [1; 2]let list4 = [10; 20; 30]
// The following line would cause a runtime error if uncommented:// let result2 = List.map2 (+) list3 list4This F# code snippet illustrates a crucial point about List.map2 when dealing with lists of different lengths.
When List.map2 is used with lists that do not have the same number of elements (like list3 with 2 elements and list4 with 3 elements), F# will throw a System.ArgumentException at runtime. This means the program will crash or stop unexpectedly because List.map2 expects both input lists to have an equal number of corresponding elements.
Unlike some other languages or functions (e.g., Python’s built-in zip function which truncates to the shortest list), List.map2 in F# does not implicitly truncate the longer list to match the shorter one.
If the desired behavior is to process elements only up to the length of the shorter list (i.e., to “truncate”), a common F# pattern is to first use List.zip to create a list of pairs, and then apply List.map to that zipped list. For example:
// Example of how to achieve truncation:// let truncatedResult = List.map (fun (x, y) -> x + y) (List.zip list3 list4)// This would correctly yield [11; 22] without an error.Sequential Implementations with Monads
Section titled “Sequential Implementations with Monads”Finally, we examine the second major category of map2 implementations: those designed for dependent, sequential processing. Unlike the independent patterns that allow for parallel execution, these implementations are necessary when the computation of the second container is affected by the result of the first.
These sequential versions are typically implemented using the bind function from a Monad. The bind operation is designed specifically to chain computations in sequence, making it a natural fit for this task.
To illustrate, let’s see how a sequential map2 can be constructed for lists using the list monad’s bind function (List.collect in F#).
F# Implementation Example
Section titled “F# Implementation Example”// This function constructs a sequential map2 using the monadic 'bind' operation.let map2Sequentially f list1 list2 = // For each element `x` from list1, bind is used to start a new computation. list1 |> List.collect (fun x -> // The new computation is a map over the entirety of list2, using the value of `x`. list2 |> List.map (fun y -> f x y) )
let numbers1 = [1; 2]let numbers2 = [100; 200]
let result = map2Sequentially (+) numbers1 numbers2// result: [101; 201; 102; 202]Analysis: Why This Leads to a Cartesian Product
Section titled “Analysis: Why This Leads to a Cartesian Product”To understand the outcome of this code, we must look at the mechanics of List.collect. This function first applies a function to every element of an input list, then flattens the resulting lists into a single output.
Execution Trace:
- The first element from
numbers1,1, is processed. The inner function maps(1 + y)over[100; 200], producing a new list:[101; 201]. - The second element,
2, is processed. The inner function maps(2 + y)over[100; 200], producing a second list:[102; 202]. - Finally,
List.collectconcatenates these generated lists into the final result:[101; 201; 102; 202].
This process, which systematically pairs every element from the first collection with every element from the second, is the definition of a Cartesian Product.
A Trivial Case?
Section titled “A Trivial Case?”This leads to a crucial insight. While this monadic implementation works, it’s often considered a “trivial” or secondary aspect when compared to map2’s primary purpose. The reason is that map2’s unique strength lies in composing independent computations, which opens the door for parallelism.
Using the strictly sequential bind function forfeits this benefit. It is a powerful tool, but in this context, it’s being used for a task that doesn’t require its full capability for complex dependency chaining. The monadic framework is flexible enough to also produce a Pointwise result if the dependency is changed to rely on an element’s position (index) instead. However, the straightforward implementation above naturally results in a Cartesian product.
Ultimately, this sequential pattern is a fallback for when independence is not possible, demonstrating that Monads encompass Applicative capabilities rather than showcasing the core identity of map2.