Understanding Functional Programming Terminology

As we delve deeper into functional programming, we encounter several key terms frequently used to describe its characteristics, such as ‘Pure Function’, ‘Side Effect’, and ‘Immutability’. However, simply listing these terms can be misleading.

This chapter critically examines the context and origin of this common FP terminology. We will explore why these terms, while seemingly convenient, can be confusing for learners. We will also see how they often arise in contrast to imperative programming rather than from pure mathematics, and why understanding this background is crucial for truly grasping the functional approach.

Key Terms Often Encountered in FP

You’ll frequently encounter the following five terms used in tutorials and textbooks, often as convenient shorthand to explain the characteristics of functional programming. Before we examine their context and potential pitfalls, let’s review the definitions commonly associated with these terms:

• Pure Function: A function that satisfies two conditions: 1) It always returns the same output for the same input. 2) It produces no side effects.
• Side Effect: An interaction with the outside world or modification of state outside the function’s local scope. Examples include modifying a global variable, writing to a file or console, reading user input, or generating a random number. FP aims to minimize and isolate side effects.
• Immutability: The property of data that cannot be changed after its creation. When you seem to “modify” an immutable data structure, you are actually creating a new structure with the changes.
• Mutability: The property of data that can be changed after creation. This is common for variables and objects in imperative and object-oriented programming.
• Referential Transparency: An expression is referentially transparent if it can be replaced with its resulting value without changing the program’s overall behavior. Pure functions guarantee referential transparency.

The Challenge: Why These Terms Can Be Confusing

A primary difficulty arises because these key terms are often used circularly, explaining each other without a firm, independent foundation. For a learner encountering them for the first time, it can feel like trying to understand a structure built in mid-air, where each part relies on another undefined part for support.

For example, “purity” might be explained using “side effects” and “referential transparency,” while “referential transparency” is explained using “purity.” Without grounding in concrete examples or familiar analogies first, the learner is left trying to understand unknown concept A using unknown concept B.

This lack of grounding is compounded when introductory materials present these terms before the underlying concepts are fully grasped through experience. Encountering unfamiliar concepts explained with equally unfamiliar jargon, defined in terms of each other, is a significant hurdle. This contributes heavily to the perception that FP is unnecessarily complex or difficult to grasp. This “jargon-first” approach, while perhaps convenient for the author, is often detrimental to the learner.

Furthermore, as we’ll explore, these terms often gain their primary meaning not in isolation, but specifically in contrast to another style of programming. This further complicates direct understanding without that comparative context.

Why This Terminology Isn’t Common in Mathematics

Despite FP’s strong mathematical roots, these specific terms (Pure Function, Side Effect, Immutability, Referential Transparency) are generally not found or used within the mathematics community itself. The primary reason is that the properties they describe are considered fundamental or simply “obvious” in a purely mathematical context.

Mathematics typically doesn’t operate within a context where state changes arbitrarily or functions interact with external systems in unpredictable ways. Therefore, mathematics doesn’t always need special terms to describe the absence of side effects or mutability – these are often the assumed norm.

Consider basic arithmetic learned in elementary school:

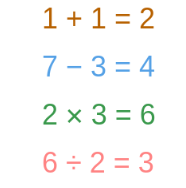
These operations inherently possess the qualities we label in FP:

• They are Pure: 1 + 1 always yields 2. The result depends only on the inputs 1 and 1.
• The values are Immutable: The number 1 doesn’t become something else during the calculation 1 + 1.
• They exhibit Referential Transparency: Any instance of 1 + 1 can be replaced by 2 anywhere without changing the outcome of a larger calculation.
• They have No Side Effects: Calculating 1 + 1 doesn’t modify some external counter or print to a screen.

We rarely, if ever, explicitly discuss these properties when learning arithmetic because they are the default, expected behavior.

While terms like “Pure Function” and “Immutability” are useful labels for programming concepts reflecting this mathematical ideal, be cautious with jargon like “Referential Transparency.” Though frequently used in FP circles, its precise meaning and utility compared to simply discussing “purity” are debated. Furthermore, its connection to origins in logic can sometimes be obscured in programming contexts. The focus should remain on the underlying principles of predictable, testable, mathematical-style computation, rather than getting lost in the terminology itself.

An Antithesis to Imperative Programming

So, if these properties are often taken for granted in mathematics, why do these terms feature so prominently in FP discussions? A key reason is that they serve as an antithesis to the concepts prevalent in Imperative Programming, which often deviates from these mathematical norms.

Most programmers first learn imperative or object-oriented styles. These paradigms typically focus on sequences of commands that modify the program’s state (mutable variables, object properties changing over time). This forms a “common sense” understanding where data changing in place and functions having broad effects (side effects) are normal and expected.

Functional programming offers a different paradigm, rooted more closely in mathematical function evaluation. Terms like “Immutability” (unchangeable data) or “Pure Function” (no side effects) gain their significance precisely because they directly challenge these common imperative assumptions. They highlight what FP avoids (in-place mutation, uncontrolled side effects) or manages differently (e.g., creating new data instead of modifying).

Therefore, learning FP often involves unlearning the imperative defaults. Terms like ‘Immutability’ or ‘Pure Function’ act as strong signposts for this necessary shift in perspective. They are, in essence, relative contrast terms, primarily meaningful when compared against the mutable state and side effects common in imperative styles.

The FP terminology arises largely because the imperative tradition introduced computational concepts that deviate from mathematical purity. This made it necessary to re-emphasize these desirable mathematical properties using explicit labels, bringing focus back to foundational principles in a computational setting.

This Book’s Stance: Avoiding Dependence on Jargon

You might notice that this book, unlike many other FP tutorials or texts, deliberately avoids heavy reliance on the five terms listed above (Pure Function, Side Effect, Immutability, Referential Transparency). We adopt this distinct approach because we believe that depending on this specific jargon to explain functional programming is fundamentally flawed.

Why? As we have emphasized throughout, functional programming is mathematics applied to computation. Explaining FP through its mathematical foundations – focusing on expressions, values, types, and function transformations – is both necessary and sufficient.

These specialized terms often lack direct mathematical counterparts. Introducing them is not only unnecessary but frequently serves to confuse rather than clarify, especially for learners.

This book aims to build understanding directly from mathematical and foundational programming principles, like those familiar from JavaScript. Therefore, we minimize reliance on terminology that exists primarily in relation to the imperative paradigm we are moving beyond.