Another Bridge Between Worlds

In our exploration of Functors, we discovered a fascinating bridge between two worlds - the world of simple functions and the world of container types. Let’s briefly recall how this bridge works.

The map Function: One Bridge We Know

To obtain a mapper function g that works with container types from our well-known function f, we used a special function called map:

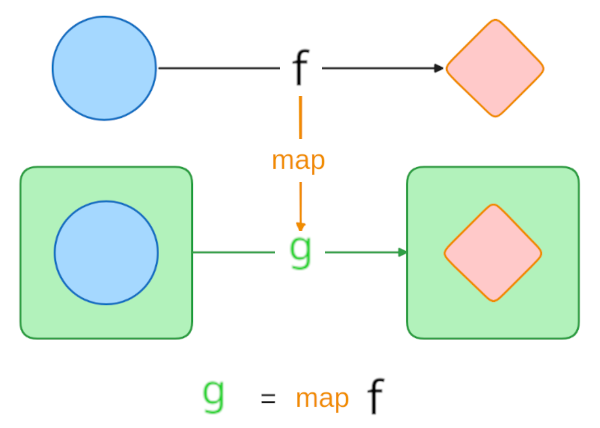
This map function serves as a bridge, transforming our simple function into one that can work with container types while preserving its essential behavior:

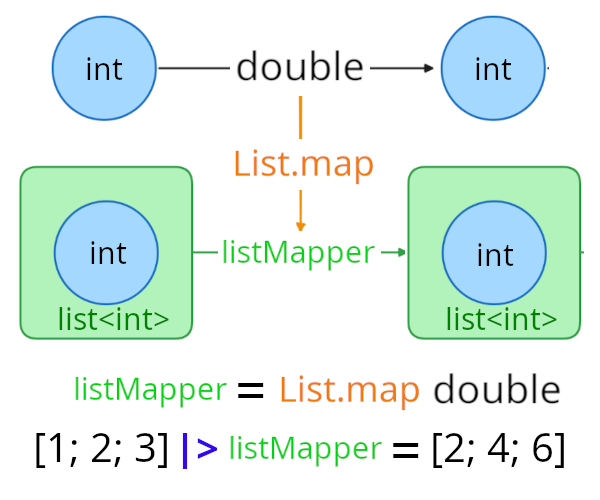
This Functor pattern has proven incredibly useful, allowing us to lift our regular functions into the world of containers. But here’s where things get intriguing - this isn’t the only way to bridge these worlds.

There exists another approach, less widely understood but often more powerful. An approach that offers a different perspective on how we can connect these two worlds. This alternative bridge is known as a Monad.

In the next chapters, we’ll uncover this mysterious second bridge and see how it provides a completely different way to think about transforming functions. We’ll discover why both bridges are necessary and how they complement each other in ways that might surprise you.