Understanding Control Flow: The Structured Programming Baseline

To understand how functional programming approaches computation, we first need a clear picture of traditional control flow structures. In this chapter, we’ll examine the foundations of structured programming that revolutionized software development.

From Simple Imperative to Structured Programming

Early programming, often referred to as simple Imperative Programming, involved giving the computer a sequence of direct commands to execute. A key characteristic of this early style was the frequent use of unconditional jumps or GOTO statements to control the flow of execution. While powerful, this often led to complex, tangled logic that was difficult to understand, debug, and maintain – sometimes called “spaghetti code.”

Structured Programming emerged in the late 1960s as a discipline to combat these issues. Pioneered by figures like Edsger W. Dijkstra, its primary goal was to improve the clarity, quality, and development time of computer programs by imposing disciplines on control flow.

The Origin and Rationale of the Three Basic Control Structures

The cornerstone of structured programming is the Structured Program Theorem (proven by Böhm and Jacopini). This theorem states that any computable algorithm, regardless of its complexity, can be implemented using only three basic control structures:

1. Sequence: This is the default control structure. Instructions are executed one after another in the order they are written.

   • Rationale: Represents the fundamental, linear progression of tasks.

2. Selection (or Branching/Conditional): This structure allows the program to choose between two or more different paths of execution based on a specific condition. Common implementations are if-then-else or switch/case statements.

   • Rationale: Essential for implementing decision-making logic within algorithms. Allows programs to react differently to different situations or data inputs.

3. Iteration (or Repetition/Looping): This structure allows a block of code to be executed repeatedly as long as a certain condition holds true (like while, do-while loops) or for a specific number of times (like for loops).

   • Rationale: Handles repetitive tasks efficiently without needing to write the same code block multiple times. Crucial for processing collections of data or performing tasks until a goal is reached.

Why These Three?

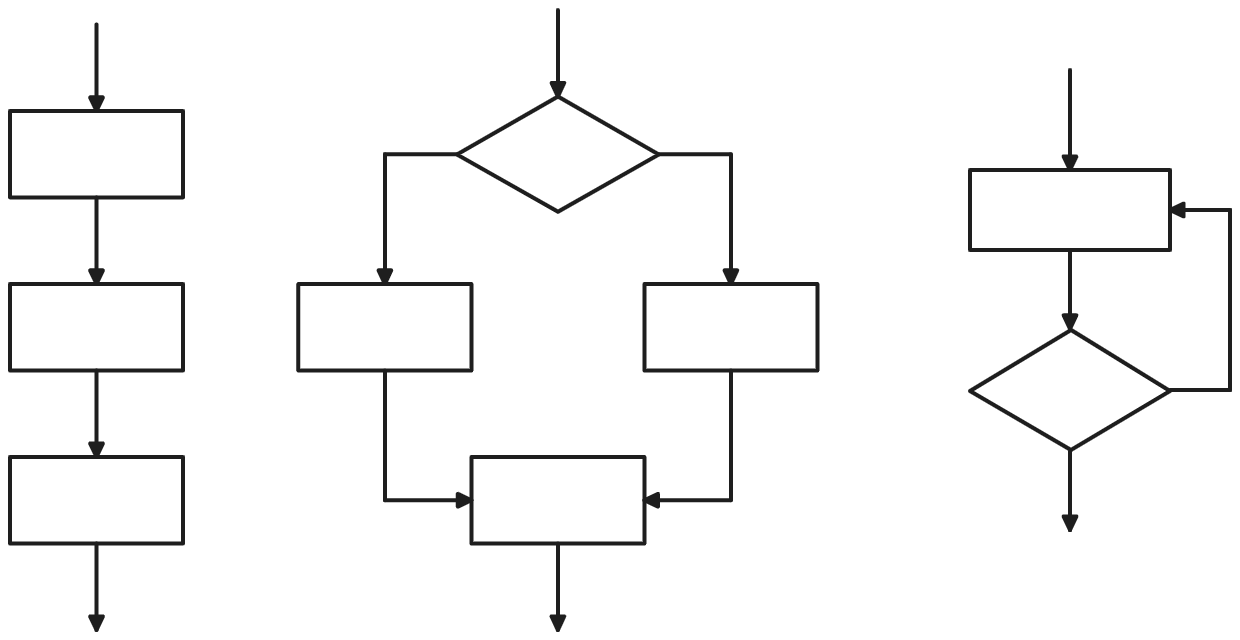
The significance of these three structures lies in their sufficiency and clarity. The Böhm-Jacopini proof demonstrated that these three are all that is mathematically necessary to express any algorithm. By restricting control flow primarily to these structures and discouraging or eliminating the use of GOTO, structured programming enforces a clearer, more predictable flow of execution. Each structure has a single entry point and a single exit point, making code blocks easier to reason about, test independently, and combine into larger programs (modularity). This leads to more maintainable, understandable, and reliable software.

Turing Completeness

The sufficiency of sequence, selection, and iteration, as demonstrated by the Structured Program Theorem, has profound implications in computer science. It essentially proves that any system or language providing these three basic control flow mechanisms possesses a powerful property known as Turing completeness.

The concept originates from the work of the mathematician and computer scientist Alan Turing, who developed a theoretical model of computation called the Turing machine. A system is considered Turing complete if it can simulate a universal Turing machine, meaning it can, in principle, perform any computation that any other computable system can perform.

The Structured Program Theorem tells us that sequence, selection, and iteration are sufficient building blocks to express any algorithm. Therefore, any programming language or computational model that effectively supports these three structures is Turing complete. This guarantees that such languages have the fundamental expressive power required for general-purpose computation. Understanding these baseline structures is crucial as we explore alternative ways to control program flow in functional programming, which, while different in style, must also ultimately provide mechanisms to achieve Turing completeness.