Category Theory

The Misplaced Emphasis on Category Theory in Functional Programming

In functional programming, concepts like Functor and Monad—which originate from category theory—are often introduced. However, it’s far more crucial for learners to first thoroughly grasp Monoid from set theory and function composition, as Functors and Monads are essentially extensions of these set-theoretic ideas. It’s much more beneficial to complete the learning process clearly within the scope of set theory.

Applying or utilizing category theory, a further level of abstract theory, in actual functional programming constitutes a separate stage of learning or research. This is likely a level that over 99% of programmers will never even engage with.

While it’s acceptable to highlight the contributions of research-level category theory to programming, we shouldn’t obscure the focus of what can be fully understood through set theory alone, nor should we confuse the vast majority of programmers, simply to provide a complete explanation of that less-than-1% domain.

It’s evident that even AI models are “contaminated” by this harmful trend in their training data, which is quite problematic.

Writing Structure:

First present the importance of category theory’s mathematical value
However, for the scope of functional programming theory and implementation level, set-theoretic understanding is necessary and sufficient
Therefore, we recommend a step-by-step approach for functional programming learning
Actually applying or utilizing category theory in functional programming is a separate stage of learning or research level

Purpose: Rather than following the myth that “mysterious” category theory is essential for true understanding of functional programming, the goal is to demonstrate that mastering Monoids and function composition in set theory is actually far more important.

Stance: Since it is an unavoidable fact that category theory itself, or concepts and terminology related to category theory, frequently appear in the context of functional programming explanations, we explain it from the stance that “knowing it will surely be helpful to avoid confusion.”

Set Theory is Bottom-Up

As we confirmed in the previous chapter, in set theory, we first define elements. Then, we create sets from those elements, and further sets from those sets, building a hierarchical structure in a bottom-up fashion.

The approach of building a theory from concrete elements before us—like 1, 2, "Hello", or true/false in programming—is naive and intuitive. This is the very essence of the type theory in simple programming languages, where types like integer and string are defined as sets of these elements.

This set-theoretic bottom-up approach is sufficient not only for functional programming but also for advanced type systems like dependent types.

The idea that things are composed of concrete “things” is known as “elemental reductionism.”

Category Theory is Top-Down

However, as a theory evolves from the concrete to the abstract, the individual elements that once seemed important lose their essential significance. The idea emerges that what is truly essential is rather the nested structure of the “containers” that hold the elements, that is, the relationships themselves.

This way of thinking is called “structuralism,” a top-down approach that seeks the essence of things in their relationships.

In category theory, the mainstream style defines things using two systems: Objects and Arrows. However, even this presupposes the existence of “things” called Objects.

But there is another, non-mainstream style: the “Arrows-only definition.” As the name implies, in this world, only Arrows exist.

So, where did the Objects go? In the Arrows-only definition, we consider a special form where an arrow points to itself, the “Identity Arrow,” and we regard this as an Object.

In other words, in this pure worldview of category theory, what exists at the root is only the relationship called Arrow, and even an Object is defined as a special relationship that “points to itself.”

Set Theory vs. Category Theory

At the heart of this argument is the question: “Do we seek the foundation of the world in independent ‘elements’ or ‘substances,’ or in ‘relationships’ and ‘structures’ themselves?”

This opposition can be framed as the conflict between “Substantialism” and “Relationalism” in Western philosophy.

1. Mathematical Foundation: The Contrast of ‘Substance’ and ‘Relation’

Set Theory: The Bottom-Up Approach 🧱

Set theory is unequivocally a bottom-up worldview.

Elements as the Origin: First, there exist “elements” (members), the smallest units of the world.
Constructing Sets: Next, these elements are gathered to create “containers” called “sets.”
Relationships Emerge: Relationships such as “maps” (functions) are defined between sets.

Everything begins with individual “things,” and larger structures are built by assembling them. It’s a very intuitive and concrete approach, like building from the ground up.

Category Theory: The Top-Down Approach 🌐

On the other hand, category theory, especially the “Arrows-only” idea, is a completely top-down approach.

Relationships as the Origin: At the beginning of the world, there are only “arrows” (morphisms). An arrow is the relationship itself that connects “something” to “something.”
Objects are Defined Later: “Objects” are defined secondarily as the “start points” or “end points” of arrows, or as arrows that do nothing (identity arrows). In other words, objects are merely “nodes” in the network of relationships.
Elements Do Not Exist: In the purest form of category theory, the concept of an “element” is unnecessary. The focus is not on what is inside an object, but only on what relationships (arrows) it has with other objects.

This is a very abstract and macroscopic approach that does not delve into the internal structure of individual things, but focuses on the structure, patterns, and relationships of the system as a whole.

This fundamental conflict of perspectives in mathematics has a surprisingly universal structure and can be found as a similar paradigm in both Western and Eastern thought.

2. Western Thought: The “Deconstruction of the Subject” by Structuralism

Next, let’s look at how Western structuralism brought a similar mode of thinking to the human sciences. What structuralism criticized was the bottom-up thinking that placed the autonomous “individual (subject)” at the center of the world.

What structuralism showed was the fact that individual consciousness and behavior are governed by an unconscious “structure” that transcends the individual. In language, the meaning of a word does not lie in the word itself, but arises from its difference (relationship) with other words within the linguistic system (structure). Here, the “subject” is not a fundamental entity like an “element” in set theory, but is “deconstructed” into a mere node that gains meaning only by being positioned within the vast network of relationships of language and culture, much like an “object” in category theory.

3. Eastern Thought: The “Negation of Substance” in “Emptiness” and “Dependent Origination”

Finally, let’s see how this relational thinking was developed in a highly sophisticated form long ago in Buddhist thought, especially in the idea of “emptiness” (Śūnyatā). What Buddhism criticized was the substantialist way of thinking that posited an unchanging, independent “self” (Ātman) and the idea that all things have their own inherent essence (Svabhāva).

Dependent Origination (Pratītyasamutpāda): The teaching that all things do not exist independently, but are provisionally established through the mutual dependence of innumerable causes and conditions (relationships).
Emptiness (Śūnyatā): As a consequence of dependent origination, it is held that all things lack an “inherent essence” that exists independently of their relationships with others. This state of lacking substance is called “emptiness.” Emptiness is not nothingness; it is the positive truth that “all things are relationships themselves.”

A “table” as an object is a bundle of innumerable relationships (dependent origination) such as “wood, carpenter, design, purpose…” and if these relationships are removed, the entity “table” disappears. This aligns surprisingly well with the idea in category theory of viewing an object as a bundle of arrows.

Conclusion

From the foregoing argument, it is clear that these three intellectual currents, while in different fields, all contain a common paradigm shift.

Field	Bottom-Up / Substantialism	Top-Down / Relationalism
Mathematics	Set Theory (Elements are primary)	Category Theory (Relationships are primary)
Western Thought	Existentialism/Humanism (The individual is primary)	Structuralism (The structure is primary)
Eastern Thought	Substantialism (Svabhāva/Ātman)	Emptiness/Dependent Origination (Interdependence is reality)

All of these are nothing less than an expression of the profound worldview that “the world is not a collection of independent ‘things,’ but is essentially a web of ‘relationships.’” We can conclude that category theory is the most rigorous and universal expression of this ancient idea in the language of modern mathematics.

The Only Tool to Construct a Category is the Relationship called Arrow

In the mainstream definition of category theory, there are two systems defined:

Object : The “thing”
Arrow : The “relationship”

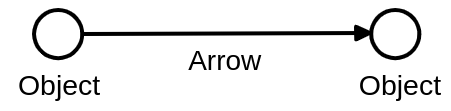
In addition, the Identity Arrow is assumed to exist trivially.

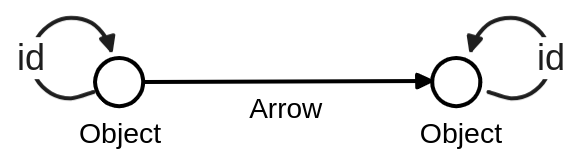
However, in the Arrows-only definition:

Object = Identity Arrow

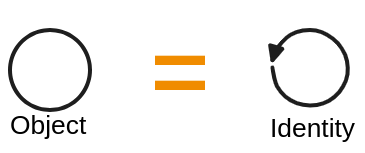
So,

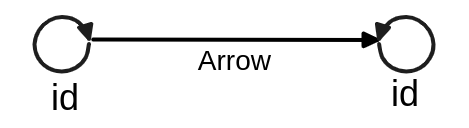
In fact, this Arrows-only definition is theoretically simpler, more beautiful, and elegant. It also purely expresses that category theory is a theoretical system that pursues only relationships in a structuralist way, as introduced at the beginning.

The Two-System Definition of Object/Arrow is Mainstream

So, why is the two-system definition of Object/Arrow mainstream, rather than the Arrows-only definition?

Ultimately, this is a trade-off between “axiomatic beauty and minimality” and “educational clarity and practical convenience.”

For many mathematicians, category theory is a “tool to be used,” so the mainstream definition, which is easy to relate to concrete examples and intuitive to handle, is overwhelmingly widely adopted. The Arrows-only definition is positioned as an elegant alternative that is important when exploring the foundations of category theory more deeply.

The Arrows-only definition is not mainstream because, compared to the mainstream Object/Arrow definition, its correspondence with concrete examples (especially set theory) is not intuitive, making it difficult to understand from an educational and practical perspective.

Reasons for the Mainstream Definition’s Adoption

Intuitive Clarity (Educational Consideration) 🧠 It is natural for humans to think in terms of “things” (objects) and their “relationships” (arrows). The mainstream definition directly corresponds to this intuition. The image of drawing dots (objects) on a blackboard and connecting them with lines (arrows) is easy for anyone to understand. The seminal work “Categories for the Working Mathematician” by one of the founders, Mac Lane, is also written with this mainstream definition, making it an educational standard.
Ease of Correspondence with Concrete Examples 🔗 The power of category theory lies in its ability to capture common structures in various fields of mathematics (set theory, group theory, topology, etc.). In these fields, the “things” being studied clearly exist.
- Set Theory: Objects are sets, arrows are maps
- Group Theory: Objects are groups, arrows are homomorphisms
- Topology: Objects are topological spaces, arrows are continuous maps
The mainstream definition is very convenient for application because it allows these “things” from concrete examples to be directly mapped to “objects” and their “relationships” to “arrows.” The Arrows-only definition requires a roundabout interpretation of first finding the “identity map” and then regarding it as a “set.”
Historical Context 📜 Category theory was originally devised by Eilenberg and Mac Lane in their study of algebraic topology to describe “functors” and “natural transformations” between different mathematical objects. What they were dealing with were precisely concrete things like topological spaces (objects) and continuous maps (arrows), and the mainstream definition was a straightforward generalization of that structure. The Arrows-only definition was a more abstract and refined form that emerged later from the quest to minimize the axioms of category theory.

Now, let’s look at the definition of a “category” in category theory, following the mainstream Object/Arrow definition.

Definition of a Category

A Category is a mathematical structure defined by a collection of Objects, a collection of Arrows (or morphisms) between those objects, and a Composition of arrows, defined by the following components and axioms.

Components of a Category

A collection of Objects A collection (class) of Objects, such as .
A collection of Arrows A collection (class) of Arrows (or morphisms), such as .
Domain and Codomain Every arrow is assigned a domain dom(f) and a codomain cod(f), which are objects. An arrow f with dom(f) = A and cod(f) = B is denoted as . The collection of all arrows from an object to an object is sometimes denoted as Hom(A, B).
Composition For any two arrows and (i.e., a pair satisfying cod(f) = dom(g)), there is a unique arrow called their composition, denoted .

Axioms of a Category

The above components must satisfy the following two axioms.

Associativity For any three composable arrows , , and , the following equality holds:
Identity For every object , there is a unique special arrow called the identity Arrow, , such that for any arrow and any arrow , the following equalities hold:

A system that satisfies these components and axioms is defined as a category.

Definition of the “Category of Sets”

The “Category of Set” is a mathematical structure with sets as objects and maps (functions) between those sets as arrows, defined by the following components and axioms.

Components of the “Category of Sets”

Collection of Objects All sets, such as .
Collection of Arrows All maps (functions), such as .
Domain and Codomain Every map has a domain set dom(f) and a codomain set cod(f). A map f with dom(f) = A and cod(f) = B is denoted as .
Function Composition For any two maps and (i.e., a pair where the codomain of f matches the domain of g), their function composition is uniquely determined.

Axioms of the “Category of Sets”

The above components satisfy the following two axioms.

Associativity For any three composable maps , , and , the following equality holds:
Identity For every set , there is a unique identity map (which maps every element to itself), such that for any map and any map , the following equalities hold:

Thus, the world of sets and maps forms a concrete category that perfectly satisfies the axioms of a category.

Function Composition: A Natural Monoid

The definition of the “Category of Sets” in category theory is identical, without any difference, to the laws we have already confirmed in the previous chapter:

Function Composition: A Natural Monoid

Monoid structure of function composition

The “Category” in Category Theory is an Abstraction of the “Category of Sets”

In fact, the axioms (rules) of category theory were created by abstracting and generalizing the properties of sets and maps (functions). Therefore, it is a natural consequence that when the definition of a category is specialized to the “Category of Set,” it fits perfectly with the rules of set theory that we are familiar with.

Let’s look at what each element of category theory corresponds to in the category of sets.

Abstract Concept in Category Theory	Concrete Counterpart in the Category of Set
Object	Set `A`, `B`
Arrow `f: A → B`	Map (function) `f: A → B`
Identity `id_A`	Identity map `id_A(x) = x`
Composition `∘`	Function composition `∘`

Based on this correspondence, let’s confirm how the axioms of category theory hold in the world of sets and maps.

1. Correspondence of the Identity Law

In category theory, it is required that for every object A, there exists an identity arrow id_A, and for any arrow f: A → B, f ∘ id_A = f and id_B ∘ f = f.

This holds perfectly in the world of sets and maps.

For every set A, there exists an identity map such that id_A(x) = x.
When composed with a map f: A → B, for any element x ∈ A, (f ∘ id_A)(x) = f(id_A(x)) = f(x), which is identical to the original map f. Similarly, id_B ∘ f is also identical to f.

2. Correspondence of the Associativity Law

In category theory, it is required that for any three arrows f, g, h for which the compositions g ∘ f and h ∘ g are possible, (h ∘ g) ∘ f = h ∘ (g ∘ f).

This is also a fundamental property of function composition.

Consider three maps: f: A → B, g: B → C, and h: C → D.
Taking any element x ∈ A:
- The left side is ((h ∘ g) ∘ f)(x) = (h ∘ g)(f(x)) = h(g(f(x)))
- The right side is (h ∘ (g ∘ f))(x) = h((g ∘ f)(x)) = h(g(f(x)))
Since both sides yield the same result for all x, the two composite maps are perfectly equal.

Thus, when the abstract definition of a category is specialized to the concrete example of the “Category of Sets,” it corresponds exactly to the laws of function composition in set theory. Category theory is a generalization that extracts only the “skeleton” of the structure created by sets and maps, so that it can be applied to various other mathematical objects (e.g., vector spaces and linear maps, topological spaces and continuous maps, etc.).

A category itself can be regarded as a sort of generalized monoid

One of the founders of Category Theory, Saunders MacLane, states in his seminal text “Categories for the Working Mathematician”:

(Source: Saunders MacLane, Categories for the Working Mathematician, 2nd ed., p. 7)

This highlights that the very foundation of Category Theory is built upon the concept of a Monoid (associative operation + identity element). Therefore, it is natural that key constructs derived from it, like Functors and Monads, are defined in a way that respects and preserves this fundamental monoidal structure inherent in composition.

The Framework of Set Theory is Sufficient

The Functors and Monads used in functional programming are indeed concepts derived from category theory, but in actual implementation and understanding, the framework of set theory is sufficient.

Historical Context:

In the category of sets Set, objects are sets and arrows are functions.
Category theory abstracted this by retaining only the concepts of objects and arrows, while discarding the concept of specific “elements.”

Essence of Abstraction:

Category of sets: There are sets A, B, and a function f: A → B.
General category: There are objects A, B, and an arrow f: A → B.
What is important is the existence of arrow composition and identity arrows; the “contents” are not questioned.

Significance of this Abstraction:

Allows other mathematical structures (topological spaces, groups, rings, etc.) to be treated within the same framework.
Provides a unified way to describe the concept of “structure-preserving maps.”
Enables discussion of “relationships between structures,” such as functors and natural transformations.

From a Practical Perspective:

A Functor can be understood as “lifting a function to a container type” (e.g., the map operation on a list).
A Monad can be treated as “wrapping a value and chaining computations” (e.g., safe computation chains with an Optional type).
In actual programming, this is sufficiently practical within the scope of a type system and function composition.

Why the Abstraction of Category Theory is Unnecessary:

The type systems of programming languages essentially operate within the category of sets (Set).
Higher-order category theory concepts like natural transformations of functors, limits/colimits, and topoi are not directly needed for everyday programming.
For implementing algorithms and ensuring type safety, a more concrete set-theoretic way of thinking is more practical.

Concrete Examples:

Scala’s Option type, Java’s Optional, and Rust’s Option type can all be understood through the set-theoretic concept of “whether a value exists or not.”
List operations (map, filter, reduce) can also be intuitively grasped as functions between sets.

While knowledge of category theory is certainly helpful for understanding the theoretical background of why these concepts “work well,” it remains a matter of general knowledge and is not essential for writing actual code. In fact, for many developers, understanding these concepts through the familiar ideas of sets and function composition is more practical.

That is why the intuition of the category of sets is sufficient when using Functors and Monads in functional programming. Since the type systems of programming languages basically operate within the category of sets, the more abstract concepts of category theory are interesting as a “theoretical background” but are not necessary in practice.

What about using the Kleisli category for Monads!?

To that counterargument, one can respond as follows:

1. The Kleisli Category is a Construction, Not a Prerequisite

The Kleisli category is constructed from an existing Monad; it is not a prerequisite for defining a Monad.
In fact, in programming languages, a Monad is first defined by its basic operations, and then the Kleisli-like structure becomes apparent.

2. At the Implementation Level, It’s a Set-Theoretic Operation

The implementation of the bind operation is ultimately the composition of functions that take a wrapped value and return another wrapped value.
This can be understood as function composition between sets, without needing to be conscious of the composition of arrows in a category.

3. The Kleisli Category is a Post-Hoc Interpretation

Programmers typically understand it as “a chain of computations with a context.”
The composition of arrows in the Kleisli category is merely a mathematical formalization of this intuitive understanding.

4. From a Practicality Standpoint

In actual error handling or state management, one can effectively use Monads without knowing the concept of the Kleisli category.
For debugging and refactoring, an understanding of types and function composition is sufficient.

5. Thinking with Concrete Examples

Chained operations with a Maybe type: if a value exists, continue to the next computation; otherwise, stop.
This behavior can be intuitively understood as a “safe chain of computations,” and can be implemented and used without knowledge of its category-theoretic background.

In short, one can argue that while the Kleisli category certainly exists, it is a “category-theoretic interpretation of a Monad,” and not the essence of a Monad in programming.

What about Haskell’s Hask category!?

To the counterargument about the Hask category, one can criticize it as “not a true category”:

1. It Does Not Satisfy the Axioms of a Category

Breakdown of Associativity: Due to undefined and infinite loops, the composition of arrows may not satisfy the associative law.
Problem with Identity Arrows: The existence of seq means that a true identity arrow does not exist (the problem of strictness).
Infinite Types: Recursive type definitions make it impossible to clearly define a true “object.”

2. It is a Product of Implementation Compromises

Due to the constraints of programming language implementation (memory, computation time), it is far from the ideal of a mathematical category.
The existence of ⊥ (bottom) pollutes the world of pure functional programming.

3. It is Merely a Convenient Metaphor

The Hask category is a convenient construction born from the desire to “explain programming with category theory.”
In reality, it is just a forced fitting of the relationship between types and functions into the framework of category theory.

4. Doubts about its Practicality

Even if one were to accept the Hask category, it brings no value to the practice of programming.
On the contrary, clinging to an incomplete category-theoretic interpretation hinders a more intuitive set-theoretic understanding.

Conclusion: The Hask category is mathematically incomplete and not practical. For understanding Functors and Monads in programming, it is healthier to use the straightforward framework of sets and functions. Category-theoretic ornamentation only adds non-essential complexity.

Extending the “Natural Monoid” of Function Composition to the Container Level

Identity Law
Associativity

Monoid structure of function composition

Functors and Monads can be seen as mechanisms for extending this basic “monoid of composition” to the container level.

A Functor extends the existing “monoid of function composition” to the container level while preserving it.
A Monad constructs a new “monoid of composition for contextual functions” at the container level.

Conclusion: The Value of Category Theory and Appropriate Learning Order

The reason we explained category theory in detail in this chapter is not to diminish its value. It is an obvious fact that concepts like Functors and Monads are derived from category theory, and it is self-evident that category theory holds great value as a powerful framework for abstraction in mathematics.

The Essence of Category Theory: A Theory of Monoid Abstraction

As MacLane himself, the founder of category theory, stated, category theory is a theoretical system that aims for abstraction while maintaining the robust properties of Monoids. The foundation of category theory lies in the Monoid structure (associativity + identity element) that function composition naturally possesses.

The development of the theory:

Monoid structure of function composition: In the category of sets, function composition naturally forms a Monoid
Abstraction through category theory: Extending to more general mathematical structures while maintaining this robust Monoid structure
Derivation of Functors and Monads: Concepts generated through this abstraction process

Position in Functional Programming

What is important in functional programming is that working within the category of sets is sufficient.

Core assertions of this chapter:

Category theory holds value as a theory of Monoid abstraction
Functors and Monads are derived from category theory, but functional programming remains within the category of sets
Abstraction to general categories is not required, so ultimately they can be understood as inheritance of the robust properties of function composition’s Monoid

Practical understanding:

Functor: Extends the Monoid of function composition to the container level while preserving it
Monad: Constructs a new Monoid for composition of contextual functions at the container level

The Importance of Learning Order

While acknowledging the value of category theory, the most effective learning order for beginners is:

Understand the natural Monoid structure of function composition
Learn the mechanism of extending it to the container level
Master implementation in set-theoretic type systems

The broader abstraction of category theory is advanced research-level content, representing a different stage of learning from practical functional programming mastery.

Conclusion: While category theory holds important value as a theory of abstraction for Monoids and function composition, understanding Functors and Monads in functional programming is most reliably and practically approached by starting from a set-theoretic foundation as extensions of the natural Monoid structure of function composition to the container level.

AI Training Data Contamination Impeding Learning Order

The data that many AI models are trained on is, in a sense, “contaminated,” exhibiting very strong biases.

I must report the fact that, even in areas that should be understood as a direct and foundational extension of set theory—areas typically of little interest to the average programmer—the importance of category theory is persistently overemphasized to an excessive degree, thereby obstructing the appropriate learning order.