Chapter 0: nullの再審 — 代数構造と型システムの歴史から解き明かす「不在」の哲学

1. 問題提起：なぜ「不在」を表現する必要があるのか

プログラミングとは、本質的に現実世界や抽象的なシステムをモデリングする行為です。そして、我々がどのようなシステムをモデル化するにせよ、値が存在しない可能性、状態が「空」と見なされる状況、あるいは操作が結果を返さない場面に必ず遭遇します。この 「不在(absence)」 という概念をいかに表現するかは、正確で堅牢なソフトウェアを構築する上で、遍在的かつ決定的に重要な要件となります。

ありふれた、具体的な例を考えてみましょう。

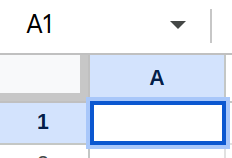
スプレッドシートの空のセル: スプレッドシートのセルは、この概念を自然に体現しています。セルは確定した値（数値、テキスト、数式）を持つこともあれば、単に空であることもあります。この空の状態はエラーではなく、その場所にデータが存在しないことを示す、スプレッドシートモデルの根源的な一部です。
アクティブなテキストエディタがない状態: Visual Studio Codeのような現代的なIDEでは、ユーザーは複数のファイルをタブで開いているかもしれませんし、すべてのタブを閉じているかもしれません。現在アクティブな、あるいはフォーカスされているテキストエディタが一つもない状態は、アプリケーションのライフサイクルにおいて完全に正当で、想定内の状態です。

これらの例が示すように、「不在」「空」「Nullity」は、単なる例外的な状況やエラーではありません。それは我々がモデリングしている領域において、現実的で、必要かつ、正当な状態なのです。したがって、我々のプログラミング言語や型システムが、この状態をいかに表現し、そしてそれと対話することを許容するかは、根源的な重要性を持つのです。

2. 理論的支柱：関数パイプラインから代数構造へ (再訪)

この「不在」を巡る議論の核心に迫る前に、我々は本書の理論的支柱となっている基本原則に立ち返る必要があります。それは、Unit 2で確立した、「関数パイプライン」 の考え方から、いかにして 「代数構造」 の定義が自然に導かれるか、という丁寧な論理の流れです。

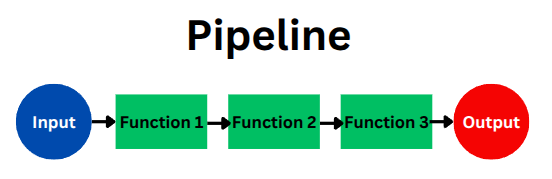
まず、我々の出発点は、データが関数の連なりを流れていく「パイプライン」という、関数型プログラミングの基本的な考え方です。

Pipeline Flow

パイプラインの構成要素:
- すべてのパイプラインは、特定の型 (Type) を持つデータを扱います。
- 関数 (Function) が、このデータを明確に定義された方法で変換します。
- これにより、我々は自然と (Type, Function) というペアを扱うことになります。
二項演算子は関数である:
- 1 + 2のような一般的な二項演算も、一種の関数である、という視点を取り入れます。例えば、+ という演算子は、(int, int) -> int という型を持つ関数と見なせます。(カリー化)
型と集合の対応:
- プログラミングにおける 型 (Type)は、数学における集合 (Set) と深く対応します。int型は整数の集合、bool型は{true, false}という集合、string型はあらゆる文字列の集合と考えることができます。

これらの洞察を統合すると、我々の目の前に明確な対応関係が浮かび上がります。

プログラミングの世界 (Pipeline)	数学の世界 (Structure)
型 (Type)	集合 (Set)
関数 (Function)	演算 (Operation)

パイプラインで扱っていた (Type, Function) のペアは、数学の世界で代数構造と呼ばれる (Set, Operation) のペアと、概念的に全く同じものだったのです。

結論として、代数構造とは、小難しい数学の話ではなく、「あるデータ型（集合）と、そのデータ型上での構造を維持する一連の操作（関数）の組み合わせ」 という、我々にとって極めて身近な設計パターンのことに他なりません。

この後の議論は、すべてこの単純かつ強力な原則の上に成り立っています。

3. nullの数学的アイデンティティ：それは「空集合」である

「不在」という概念は、単なるソフトウェア開発上の都合から生まれたものではなく、数学に深いルーツを持っています。プログラミングにおいて null が表現している概念は、特に集合論 (Set Theory) における根源的な構造と、直接的かつ強力に対応します。

空集合 (Empty Set): 公理的集合論において、空集合 (∅ または {}) は、元を一切含まない集合として一意に定義されます。それは他のあらゆる集合や数学的対象を構築するための土台となる、理論の礎です。null という概念は、この空集合と直接的に類似するものと見なすことができます。すなわち、ある型（その型が取りうる値の集合と見なす）の中に、いかなる値も存在しない状態を表すのです。

この繋がりは、極めて重要です。それは、null が単なるプログラミングの便宜のために発明された問題含みの値なのではなく、実際には数学において明確に定義された、不可欠な概念に対応することを示唆しているからです。本書における我々の視点は、型は集合圏 (Category of Sets) における対象（オブジェクト）であり、関数はその間の射（モーフィズム）である、というものです。

4. “億万ドルの間違い”の真相

その概念的・数学的な正当性にもかかわらず、null参照、特に多くの初期のオブジェクト指向言語や手続き型言語に実装されたそれは、頻繁でデバッグ困難な実行時エラーを引き起こすことで悪評を得ました。Javaの NullPointerException、C#の NullReferenceException、C/C++のセグメンテーションフォルトなど、誰もが恐れるエラーです。

プログラミング言語設計のパイオニアであるアントニー・ホーア卿は、1965年頃にALGOL Wでnull参照を導入したことを、彼の「億万ドルの間違い」と呼び、嘆いたことは有名です。

私はそれを「億万ドルの間違い」と呼んでいます。それは1965年のnull参照の発明でした…。これは数え切れないエラー、脆弱性、そしてシステムのクラッシュを引き起こし、過去40年間でおそらく10億ドルもの苦痛と損害をもたらしたでしょう。

この強力な物語は広く受け入れられ、プログラミング界の多くの場所で、nullという概念自体が本質的に欠陥があり危険なものである、という確信を植え付けました。

しかし、ここで我々は、「代数構造とは (集合, 演算) のペアである」という原則に立ち返り、批判的な再評価を行わなければなりません。

真の間違いは、「不在」を表現するという根源的な概念（null、空集合のアナロジー）だったのでしょうか？それとも、その根源的な概念を、壊滅的な実行時エラーなしに管理するための、適切な言語メカニズムの完全なる欠如 — すなわち、nullを許容する型と許容しない型を区別できる堅牢な型システムや、nullの可能性がある値を安全に扱うための演算子の欠如 — こそが間違いだったのでしょうか？

本書は、後者を強く主張します。「億万ドルの間違い」とは、nullの存在そのものではなく、nullを受け取った際に実行すべき**「安全な演算」が言語レベルで定義されていなかったことに他なりません。代数構造の観点から言えば、null（空集合）とペアになるべき代数構造（＝対応する安全な演算）を設計し忘れたこと**、これこそが間違いの真相なのです。

5. 歴史的帰結としての`Option`型

チェックされないnull参照がもたらす危険に直面し、関数型プログラミングのコミュニティ、特にHindley-Milner (HM) 型システムにルーツを持つ言語（ML、Haskell、そして初期F#に影響を与えた）は、異なる解決策を支持しました。それは、言語の核から広範なnull参照を排除し、オプショナルな値を Option型（HaskellではMaybe）を用いて型システム内で明示的に表現することです。

Option<T>型は、通常、代数的データ型 (ADT) — 合計型 (Sum Type) — として定義され、2つのケースを持ちます。

Some T: T型の値が存在することを示す。
None: 値が存在しないことを示す。

このアプローチの最大の利点は、型システムによって強制されるコンパイル時の安全性です。Option<T>はTとは異なる型であるため、プログラマはOption<T>型の値を、誤ってT型であるかのように使用することはできません。型システムは、パターンマッチなどを通じてSomeとNoneの両方のケースを明示的に処理することを義務付け、これによりコンパイル時にnull参照エラーを防ぎます。

しかし、Option型はHMの枠組み内でnullポインタ問題を解決する一方で、それ自身の新たな帰結と批判的な視点を生み出しました。

批判1 (構造的複雑性): Option<T>は単一レベルのオプショナルな値をエレガントに扱いますが、Option<Option<T>>のようにネストすると、それが表現しようとしている単純な「有無」以上に複雑な構造に感じられることがあります。
批判2 (哲学的・歴史的正当性): nullのような概念を完全に排除することは、本当に理論的に最も健全な道だったのでしょうか？それは「nullは悪である」という神話への過剰反応ではなかったでしょうか？
批判3 (HMの設計思想と制約): HMベースの言語でOptionが普及したことは、HM型システム自体の技術的な特性と限界に深く結びついています。

Note: 技術的・歴史的深掘り – HMシステム、Null、Option、共用体型

Hindley-Milner(HM)ベースの言語が、暗黙的なnullよりもOption/Maybe型を強く支持した歴史的経緯は、HMの核となる設計目標（健全性と型推論）と、そのアルゴリズム的機構（単一化、代数的データ型との親和性）に深く根ざしています。

標準的なHMは、T | nullのようなタグなし共用体型やサブタイピングをネイティブに統合するには、理論的および実践的に大きなハードルを抱えています。HMのアルゴリズムは、型変数を具体的な型に「単一化（unify）」していくことで型推論を行いますが、T | nullのような型は、nullが全ての参照型に暗黙的に代入可能（サブタイプ）であると解釈されるため、単純な単一化アルゴリズムを複雑にし、健全性を損なうリスクがありました。

一方で、Option<T>のような代数的データ型（ADT）は、Some(T)とNoneという明確にタグ付けされたコンストラクタを持つため、HMのパターンマッチングと単一化アルゴリズムにとって非常に自然な構造でした。コンパイラは、型がOption<T>であることを明確に認識し、プログラマに両方のケースを処理するよう強制できます。

つまり、Option/Maybeは、HMの設計目標とアルゴリズム的制約にとって最も自然な道だったのです。T | nullのような共用体型/サブタイピングをHMに直接統合することは、理論的・実践的に大きな挑戦でした。この困難はHMの特定の形式化に固有のものであり、Optionを使わずに「不在」を健全な型システムで扱うことが理論的に不可能というわけではありません。しかし、それはHMが選択した道ではありませんでした。

このHMの制約が、意図せずして「nullは悪である」という物語を補強し、nullのような概念を保持しつつ安全性を確保する別の健全なアプローチの探求を妨げた可能性があるのです。

6. もう一つの道：TypeScriptが証明した「安全なnull」

HMベースの言語がOption型を採用した一方で、TypeScriptのような言語によって異なる道筋が成功裏に示されました。これは、「null自体が管理不能な“億万ドルの間違い”である」という物語を再考するよう我々に促します。

TypeScriptは、nullとundefinedをNullable共用体型（例: string | null）として型システムに統合し、型ガード（例: if (value !== null)) やオプショナルチェイニング (?.) といったメカニズムを提供することで、高度な実践的null安全性を達成しました。プログラマはnullの可能性がある値を扱うことができ、コンパイラは洗練されたコントロールフロー分析を通じて、多くの一般的なnull参照エラーをコンパイル時に防ぐ手助けをします。

function processText(text: string | null): void {
    if (text !== null) {
        // このブロック内では、TypeScriptは'text'が'string'であることを知っている
        console.log(`Length: ${text.length}`);
    } else {
        console.log("No text provided.");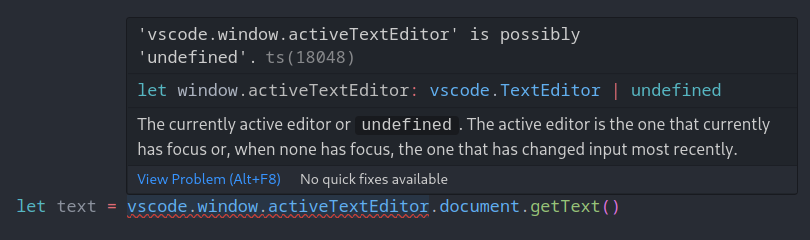
    }
}

TypeScriptのこの成功は、重要な問いを提起します。もしnull可能性が適切な型システムの機能によって効果的に管理できるのであれば、なぜHMの伝統はOption型をかくも強く支持したのでしょうか？問題は本当にnull自体にあったのか、それとも古典的なHMの型推論が持つ特有の限界にあったのか？ Option型だけが唯一の解ではないことは明らかです。

7. `Timeline`の哲学：理論的正当性と実践的単純性の両立

これまでの分析 — nullの根源的な性質（空集合）、Optionアプローチの歴史的文脈と潜在的な欠点、そしてTypeScriptが示した実践的な成功 — に基づき、このTimelineライブラリは、「不在」を扱うための特定の、意図的な哲学を採用します。

我々は、nullを値の不在を表す主要な表現として受け入れ、それを安全に扱うための厳格な規律と組み合わせる。

この選択は、以下の理由によって正当化されます。

理論的正当性: nullを「空集合」と見なす数学的整合性と一致します。これはnull自体が理論的に無効であるという前提を拒絶し、安全性はそれがどのように扱われるかによって決まる、という立場を取ります。
単純性と直接性: Option型がネストした際の潜在的な構造的複雑性を回避します。値が存在するか、nullであるか。これはスプレッドシートの空のセルのような状態を直接的に反映し、単純なデータ構造とロジックに繋がります。
規律による安全性: TypeScriptが成功したモデルに倣い、nullは許容されますが、その使用は安全性を保証するメカニズムによって保護されなければなりません。このライブラリにおける「安全なメカニズム」とは、nullの可能性があるTimelineから値を取得する際に、常にヘルパー関数 isNull を使ってチェックするという、利用者に課せられた厳格な規律と規約です。

この規律あるパターンこそが、我々のフレームワークにおける必要不可欠な「安全な演算」であり「ガードレール」として機能します。この規約に従うことで、歴史的にnullと関連付けられてきた危険は、このライブラリの使用文脈において効果的に緩和されるのです。

我々はこのアプローチを、HM/Optionの伝統から意識的に分岐し、概念の明快さと表現の単純性を優先する、理論的に有効な道として位置づけています。この章で確立した哲学は、続く章で紹介するcombineLatestWithのようなAPIの設計に直結し、この規律あるnullへのアプローチが、いかに明確で予測可能なリアクティブシステムを構築するかに繋がっていきます。