Bringing It All Together: Functor & Monad (Revisit)

Our ultimate goal has been to obtain a mapper function that can work between container types:

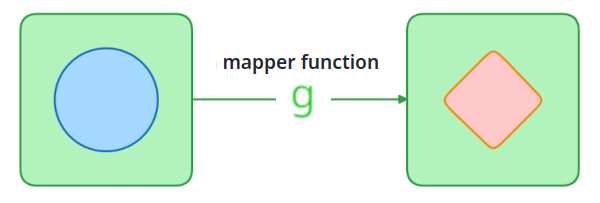
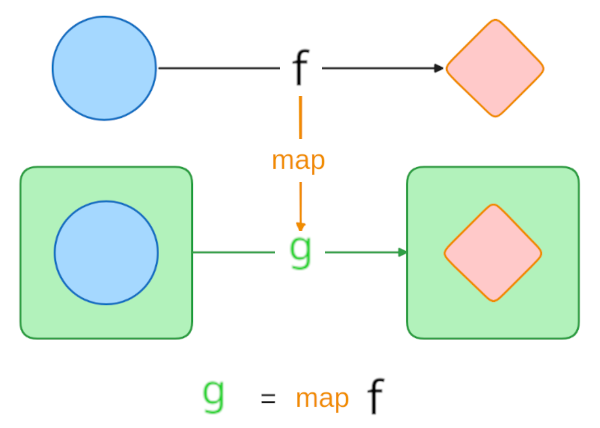
We first learned one way to achieve this - using Functor’s map to lift a regular function into the world of containers:

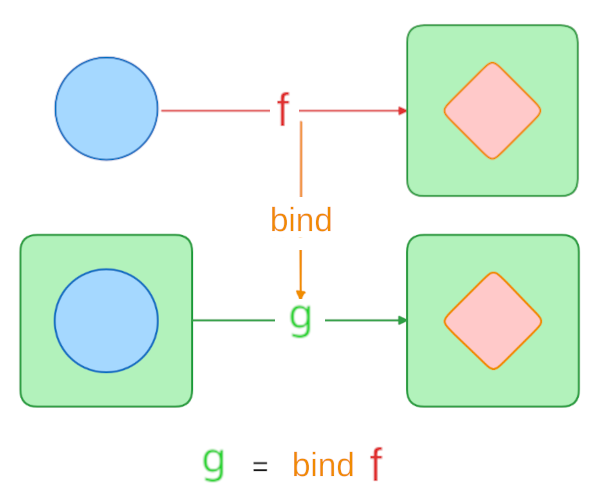
And we also discovered another path - using Monad’s bind to transform a Kleisli arrow into a container mapper:

Two Bridges, One Structure

Now we can see two distinct approaches for obtaining a container mapper function:

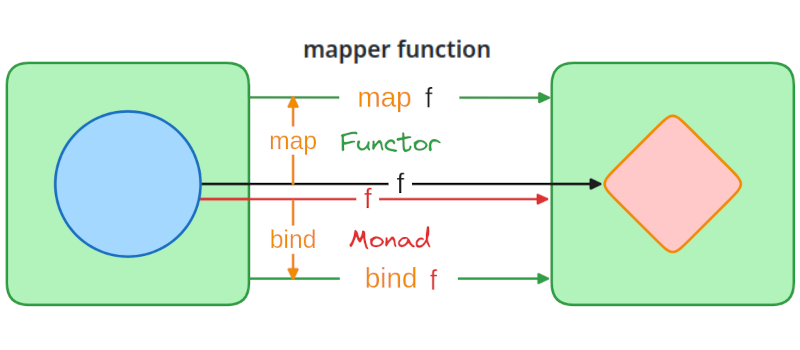
This unified view reveals an elegant symmetry in how we can obtain our desired mapper function g:

• The Functor approach (upper path) obtains g by using map to transform a regular function f into a container mapper function g / map f
• The Monad approach (lower path) obtains g by using bind to transform a Kleisli arrow f into a container mapper function g / bind f

Both paths provide us with what we ultimately want - a function g that can map between containers. The difference lies in our starting point: we can begin with either a regular function or a Kleisli arrow, and both paths will lead us to the container mapper function we seek.