圏論（Category Theory）

関数型プログラミングにおける圏論の誤った強調

関数型プログラミングでは、圏論に由来するFunctorやMonadといった概念がしばしば導入されます。しかし、学習者にとっては、FunctorやMonadが実質的にこれらの集合論的なアイデアの拡張であるため、まず集合論におけるMonoidと関数合成を徹底的に理解することの方がはるかに重要です。集合論の範囲内で学習プロセスを明確に完結させる方が、はるかに有益です。

実際の関数型プログラミングにおいて、さらに抽象的な理論である圏論を適用したり利用したりすることは、学習や研究の別の段階を構成します。これはおそらく、99%以上のプログラマーが決して関わることのないレベルでしょう。

研究レベルの圏論がプログラミングに貢献したことを強調するのは許容できますが、集合論だけで完全に理解できることの焦点を曖昧にしたり、1%にも満たない領域の完全な説明を提供するためだけに、大多数のプログラマーを混乱させるべきではありません。

AIモデルでさえ、この有害な傾向によって学習データが「汚染」されているのは明らかであり、これは非常に問題です。

本章のアプローチとスタンス

執筆構造：

• まず圏論の数学的価値の重要性を提示する
• しかし、関数型プログラミング理論の範囲と実装レベルにおいては、集合論的理解が必要かつ十分である
• したがって、関数型プログラミング学習では段階的アプローチを推奨する
• 圏論を関数型プログラミングに実際に適用または活用することは、別段階の学習または研究レベルである

目的： 「神秘的な」圏論が関数型プログラミングの真の理解に必須であるという神話に従うのではなく、実際には集合論におけるMonoidと関数合成を習得する方がはるかに重要であることを実証することが目標である。

スタンス： 圏論そのもの、または圏論に関連する概念や用語が関数型プログラミングの説明の文脈で頻繁に現れることは避けられない事実であるため、「それを知っていれば混乱を避けるのに確実に役立つだろう」というスタンスで説明している。

集合論（Set theory）はボトムアップ

前の章で確認した通り、集合論では、まず最初に要素を定義します。そしてその要素から集合を作り、さらにその集合を元にした集合を……というように、階層構造をボトムアップで構築していきます。

集合論のように目の前にある具体的な要素――プログラミングで言えば 1 や 2、"Hello"、true/false といったデータ――から理論を積み上げていく手法は、素朴で直感的です。それらの集合として整数型や文字列型といった型（Type）が定義される、素朴なプログラミング言語の型理論そのものです。

関数型プログラミングはもちろん、依存型（Dependent type）のような高度な型システムにおいても、この集合論的なボトムアップのアプローチで十分に対応可能です。

物事は具体的なモノから構成されると考えるのが 「要素還元主義」 です。

圏論（Category theory）はトップダウン

しかし、理論が具体から離れて抽象へと進化するにつれ、かつて重要だと思われた個々の要素は、その本質的な重要性を失っていきます。真に本質的なのは、むしろ要素を収める「入れ物」が持つ入れ子構造、すなわち関係性そのものである、という考え方が生まれます。

このような考え方は 「構造主義」 と呼ばれ、物事の本質を関係性に求めるトップダウンのアプローチです。

圏論では、対象（Object）と射（Arrow）の2系統で定義するスタイルが主流ですが、これですらなお、Objectという「モノ」の存在を前提としています。

しかし、主流ではないもう一つのスタイルに 「Arrows-only定義」 があります。その名の通り、この世界に存在するものは 射（Arrow） だけです。

では、Objectはどこへ行ったのでしょうか。Arrows-only定義では、射が自分自身を指し示す 「恒等射（Identity Arrow）」 という特別な形態を考え、これを Objectと見なします。

つまり、この純粋な圏論の世界観では、根源的に存在するのはArrowという関係性のみであり、Objectでさえも 「自分自身を示す」という特別な関係性 として定義されるのです。

---

集合論 vs 圏論

この論証の中心にあるのは、 「世界の根源を、独立した『要素』や『実体』に求めるのか、それとも『関係性』や『構造』そのものに求めるのか」 という問いです。

この対立は、西洋哲学における「実体論（Substantialism）」と「関係論（Relationalism）」の対立として整理できます。

1. 数学的基礎：『実体』と『関係』の対比

集合論：ボトムアップのアプローチ 🧱

集合論は、まさしくボトムアップの世界観です。

1. 要素が原点: まず、世界の最小単位である 「要素（元）」 が存在します。
2. 集合を構成: 次に、その要素を集めて 「集合」 という「入れ物」を作ります。
3. 関係が生まれる: 集合と集合の間に「写像（関数）」などの 関係 が定義されます。

すべては個々の「モノ」から始まり、それらを組み立ててより大きな構造を作っていくという、非常に直感的で具体的なアプローチです。基礎から一つずつ積み上げていくイメージですね。

---

圏論：トップダウンのアプローチ 🌐

一方、圏論、特に「Arrows-only」の考え方は、完全な トップダウン です。

1. 関係性が原点: 世界の始まりには 「射（Arrow）」 しかありません。射は「何か」と「何か」をつなぐ関係性そのものです。
2. 対象は後から定義される: 「対象（Object）」 は、射の「始点」や「終点」として、あるいは何もしない射（恒等射）として、二次的に定義されます。つまり、対象は関係性の「結節点」のような存在にすぎません。
3. 要素は存在しない: 圏論の最も純粋な形では、「要素」という概念は必要ありません。対象の中に何が入っているかを問うのではなく、対象が他の対象とどのような関係（射）で結ばれているかだけが重要です。

これは、個々のモノの内部構造には立ち入らず、システム全体の構造やパターン、関係性そのものに注目する、非常に抽象的で大局的なアプローチと言えます。

---

この数学における根源的な視点の対立は、驚くほど普遍的な構造を持っており、西洋と東洋の思想にも同様のパラダイムとして見出すことができます。

2. 西洋思想：構造主義による「主体の解体」

次に、西欧の構造主義が、圏論と同様の思考様式を人間科学に持ち込んだことを見ます。構造主義が批判したのは、自律的な「個人（主体）」を世界の中心に据えるボトムアップ的な思想でした。

構造主義が示したのは、個人の意識や行動は、個人を超えた無意識的な 「構造」 によって規定されている、という事実です。言語において、単語の意味はそれ自体にあるのではなく、言語体系という「構造」の中での他の単語との差異（関係性）によって生じます。ここにおいて、「主体」は集合論の「要素」のような根源的実体ではなく、圏論の「対象」のように、言語や文化という巨大な関係性のネットワークの中に位置づけられることでのみ意味を持つ、結節点のような存在へと「解体」されます。

3. 東洋思想：「空」と「縁起」における「実体の否定」

最後に、この関係主義的思考が、仏教思想、特に「空」の思想において、遥か昔から極めて洗練された形で展開されていたことを見ます。仏教が批判したのは、不変で独立した「自己（我）」や、事物に固有の「本質（自性）」を想定する実体論的な考え方でした。

• 縁起: あらゆる事物は、単独で存在するのではなく、無数の原因や条件（＝関係性）が相互依存することで仮に成立している、という思想です。
• 空: 上記の縁起の帰結として、あらゆる事物は、他との関係性を離れて独立して存在する「固有の本質」を持たない、とされます。空とは「無」ではなく、「あらゆるものが関係性そのものである」 という積極的な真理を指します。

テーブルという「対象」は、「木材、設計図、大工…」といった無数の 関係性（縁起）の束 であり、関係を取り除けば「テーブル」という実体は消え去ります。これは、対象を射の束として捉える圏論の思想と驚くほど一致します。

結論

以上の論証から、この三つの思想潮流は、それぞれ異なる分野にありながら、共通のパラダイムシフトを内包していることが明らかです。

分野	ボトムアップ・実体論	トップダウン・関係論
数学	集合論（要素が根源）	圏論（関係性が根源）
西洋思想	実存主義・人間主義（個人が根源）	構造主義（構造・関係性が根源）
東洋思想	実体論（自性・我）	空・縁起（相互依存・関係性が根源）

これらはすべて、 「世界は独立した『モノ』の集まりではなく、本質的に『関係性』の網の目である」 という、深遠な世界観の表明に他なりません。圏論は、この古代からの思想を、現代数学の言語で最も厳密かつ普遍的に表現したものと結論づけることができます。

圏論を構成する道具立てはArrowという関係だけ

圏論の主流の定義では、

• Objectというモノ
• Arrowという関係

の2系統定義

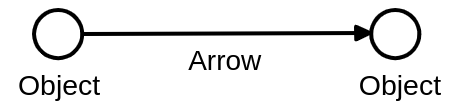
加えて、Identit Arrowが自明に存在するとされる。

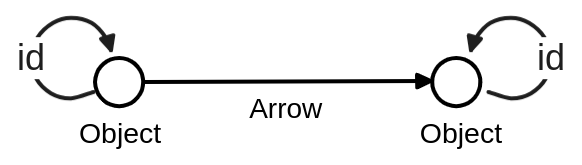
しかし、Arrows-only定義では、

Object = Identity Arrow

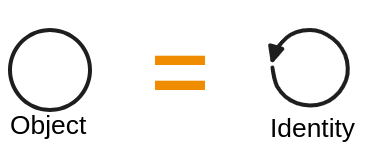
なので

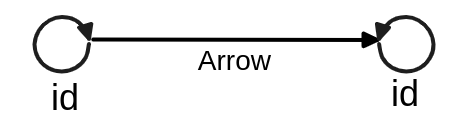
実際に、このArrows-only定義のほうが理論的にはシンプルで美しくエレガントになるし、最初に紹介したとおり、圏論とは構造主義的に関係性のみを追求する理論体系であることも純粋に表現できています。

Object/Arrowの2系統の定義が主流

それでは、なぜArrows-only定義のほうではなく、Object/Arrowの2系統の定義が主流になっているのでしょうか？

結局のところ、これは 「公理的な美しさと最小性」と「教育的な分かりやすさと応用上の利便性」 のトレードオフです。

圏論は多くの数学者にとって「使うための道具」であるため、具体例との対応が分かりやすく、直感的に扱える主流の定義が圧倒的に広く採用されています。Arrows-only定義は、圏論の基礎をより深く探求する際に重要な、エレガントな代替案という位置づけです。

Arrows-only定義が主流になっていないのは、主流のObject/Arrow定義に比べて、具体例（特に集合論）との対応が直感的でなく、教育的・実践的な観点から分かりにくいためです。

---

主流定義が採用される理由

1. 直感的な分かりやすさ（教育的配慮） 🧠 人間は「モノ（対象）」と、それらの「関係（射）」で物事を考えるのが自然です。主流の定義は、この直感に直接的に合致します。黒板に点を描き（対象）、それらを線で結ぶ（射）というイメージは、誰にとっても理解しやすいものです。創始者の一人であるマックレーンの名著『圏論の基礎』も、この主流の定義で書かれており、教育的な標準となっています。

2. 具体例との対応付けの容易さ 🔗 圏論の力は、数学の様々な分野（集合論、群論、位相空間論など）に共通する構造を捉える点にあります。これらの分野では、研究対象となる「モノ」が明確に存在します。

   • 集合論: 対象は集合、射は写像
   • 群論: 対象は群、射は準同型写像
   • 位相空間論: 対象は位相空間、射は連続写像

   主流の定義は、これらの具体例の「モノ」をそのまま「対象」に、「関係」をそのまま「射」に対応させられるため、応用する際に非常に便利です。Arrows-only定義では、まず「恒等写像」を見つけ出し、それを「集合」と見なす、という回りくどい解釈が必要になります。

3. 歴史的な経緯 📜 圏論は元々、アイレンベルグとマックレーンが代数的位相幾何学の研究の中で、異なる数学的対象間の「関手」や「自然変換」を記述するために考案されました。彼らが扱っていたのは、まさに位相空間（対象）や連続写像（射）といった具体的なものであり、その構造を素直に一般化したのが主流の定義でした。Arrows-only定義は、その後に圏論の公理をいかに最小化できるか、という探求から生まれた、より抽象度の高い洗練された形式です。

それでは、主流のObject/Arrow定義に従って、圏論における「圏」の定義を見ていこう。

---

圏の定義

圏（Category） とは、対象（Object） の集まりと、その対象間の 射（Arrow） の集まり、そして射の 合成（Composition） が定められた数学的構造であり、以下の構成要素と公理によって定義されます。

圏の構成要素

1. 対象の集まり といった対象（Object）の集まり（クラス）。

2. 射の集まり といった射（Arrow）の集まり（クラス）。

3. ドメインとコドメイン すべての射 には、その始点となるドメイン（domain） dom(f) と、終点となるコドメイン（codomain） cod(f) と呼ばれる対象がそれぞれ一つずつ割り当てられています。dom(f) = A かつ cod(f) = B である射 f を、 と表記します。 ある対象 から対象 へのすべての射の集まりを Hom(A, B) と表記することもあります。

4. 合成 任意の2つの射 と （すなわち、cod(f) = dom(g) を満たすペア）に対して、その合成（composition）と呼ばれる射 がただ一つ定まります。

---

圏の公理

上記の構成要素は、以下の2つの公理を満たさなければなりません。

1. 結合法則 (Associativity) 合成が可能な任意の3つの射 , , に対して、以下の等式が成り立ちます。

2. 単位法則 (Identity) すべての対象 に対して、恒等射（identity Arrow）と呼ばれる特別な射 がただ一つ存在し、任意の射 と任意の射 に対して、以下の等式が成り立ちます。

以上の構成要素と公理を満たす体系が、圏として定義されます。

「集合の圏」の定義

「集合の圏」（Category of Set）とは、集合 を対象とし、その集合間の 写像（関数） を射とする数学的構造であり、以下の構成要素と公理によって定義されます。

「集合の圏」の構成要素

1. 対象の集まり といった、すべての集合。

2. 射の集まり といった、すべての写像（関数）。

3. ドメインとコドメイン すべての写像 には、その定義域であるドメインの集合 dom(f) と、値域であるコドメインの集合 cod(f) があります。dom(f) = A かつ cod(f) = B である写像 f を、 と表記します。

4. 関数の合成 任意の2つの写像 と （すなわち、f のコドメインと g のドメインが一致するペア）に対して、その関数の合成 がただ一つ定まります。

---

「集合の圏」の公理

上記の構成要素は、以下の2つの公理を満たします。

1. 結合法則 (Associativity) 合成が可能な任意の3つの写像 , , に対して、以下の等式が成り立ちます。

2. 単位法則 (Identity) すべての集合 に対して、恒等写像 （すべての要素 を 自身に対応させる写像）がただ一つ存在し、任意の写像 と任意の写像 に対して、以下の等式が成り立ちます。

以上の通り、集合と写像の世界は、圏の公理を完全に満たす一つの具体的な圏を形成しています。

Function Composition: A Natural Monoid

圏論の 「集合の圏」の定義 とは、すでに我々が前の章

Function Composition: A Natural Monoid

で確認した法則と寸分違わない同じものです。

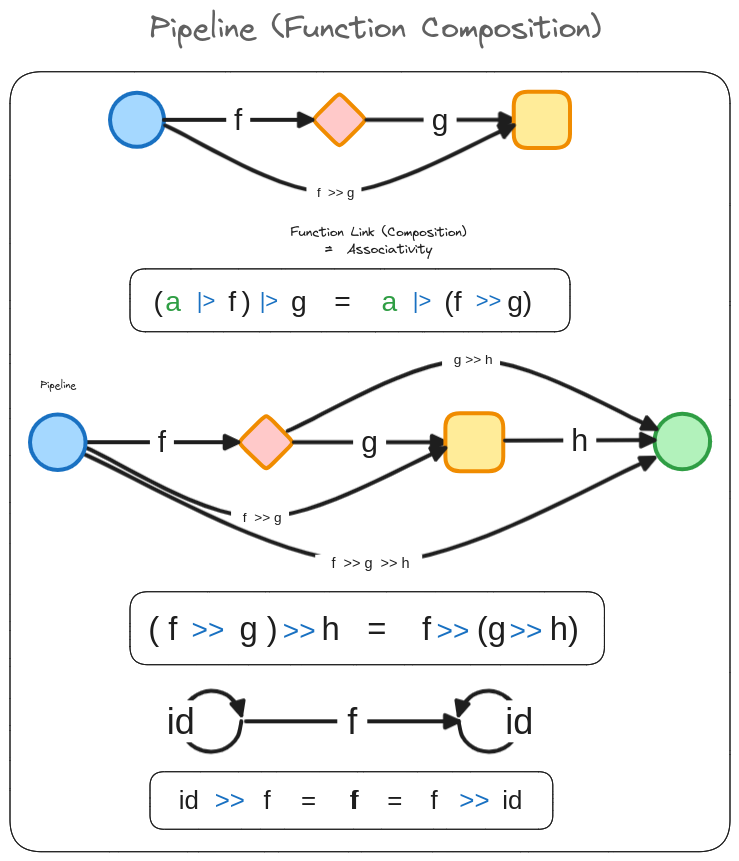
圏論の「圏」とは「集合の圏」を抽象化したもの

実は、圏論の公理（ルール）は、集合と写像（関数）が持つ性質を抽出・一般化して作られたものです。ですから、圏論の定義を「集合の圏 (Category of Set)」に具体化すると、私たちがよく知る集合論のルールにぴったりと収まるのは、当然の帰結と言えます。

具体的に、圏論の各要素が、集合の圏で何に対応するかを見てみましょう。

圏論の抽象的な概念	集合の圏 (Set) での具体的な対応物
対象 (Object)	集合 A, B
射 (Arrow) f: A → B	写像（関数） f: A → B
恒等射 (Identity) id_A	恒等写像 id_A(x) = x
合成 (Composition) ∘	写像の合成 ∘

この対応関係をもとに、圏論の公理が集合と写像の世界でどのように成り立つかを確認します。

1. 単位法則 (Identity Law) の一致

圏論では、すべての対象 A に恒等射 id_A が存在し、任意の射 f: A → B に対して f ∘ id_A = f かつ id_B ∘ f = f であることを要請します。

これは集合と写像の世界で完璧に成り立ちます。

• すべての集合 A には、id_A(x) = x となる恒等写像が存在します。
• 写像 f: A → B と合成すると、任意の要素 x ∈ A に対して (f ∘ id_A)(x) = f(id_A(x)) = f(x) となり、元の写像 f と全く同じです。 id_B ∘ f も同様に f と一致します。

2. 結合法則 (Associativity) の一致

圏論では、合成 g ∘ f と h ∘ g が可能な任意の3つの射 f, g, h に対して、(h ∘ g) ∘ f = h ∘ (g ∘ f) であることを要請します。

これも写像の合成が持つ基本的な性質です。

• f: A → B, g: B → C, h: C → D という3つの写像を考えます。
• 任意の要素 x ∈ A を取ると、
  • 左辺は ((h ∘ g) ∘ f)(x) = (h ∘ g)(f(x)) = h(g(f(x)))
  • 右辺は (h ∘ (g ∘ f))(x) = h((g ∘ f)(x)) = h(g(f(x)))
• 両者はすべての x について同じ結果を返すため、2つの合成写像は完全に等しくなります。

このように、圏論の抽象的な定義は、具体例である「集合の圏」に特殊化すると、集合論における写像の合成法則と寸分違わず対応します。圏論は、この集合と写像が作る構造を「骨格」だけ抜き出して、他の様々な数学的対象（例：ベクトル空間と線形写像、位相空間と連続写像など）にも当てはめられるように一般化したものなのです。

A category itself can be regarded as a sort of generalized monoid

圏論の創始者の一人であるソーンダース・マックレーンは、その独創的なテキスト『圏論の基礎』で次のように述べています。:

(Source: Saunders MacLane, Categories for the Working Mathematician, 2nd ed., p. 7)

これは、圏論のまさにその基礎が、Monoidの概念（結合的な演算 + 単位元）の上に築かれていることを浮き彫りにしています。したがって、そこから導かれるファンクターやモナドのような主要な構成概念が、合成に内在するこの根源的なモノイド構造を尊重し、保存する方法で定義されるのは自然なことです。

集合論の枠組みだけで事足りる

関数型プログラミングで使われるFunctorやMonadは、確かに圏論由来の概念ですが、実際の実装や理解においては集合論の枠組みで十分事足ります。

---

歴史的経緯：

• 集合の圏Setでは、対象が集合、射が関数
• これを抽象化して、対象と射の概念だけを残し、具体的な「要素」の概念を捨象したのが圏論

抽象化の本質：

• 集合の圏：集合 A, B があり、関数 f: A → B がある
• 一般の圏：対象 A, B があり、射 f: A → B がある
• 重要なのは射の合成と恒等射の存在で、「中身」は問わない

この抽象化の意義：

• 集合以外の数学的構造（位相空間、群、環など）も同じ枠組みで扱える
• 「構造を保つ写像」という概念を統一的に記述できる
• 関手や自然変換といった「構造間の関係」を論じられる

実用的な観点から：

• Functorは「コンテナ型に対する関数の持ち上げ」として理解できる（リストに対するmap操作など）
• Monadも「値の包装と連鎖的な計算」として扱える（Optional型での安全な計算連鎖など）
• 実際のプログラミングでは、型システムと関数合成の範囲で十分実用的

圏論の抽象化が不要な理由：

• プログラミング言語の型システムは基本的に集合の圏（Set）内で動作する
• 関手の自然変換、極限・余極限、トポスなどの高次の圏論的概念は、日常的なプログラミングでは直接必要ない
• アルゴリズムの実装や型安全性の確保において、より具体的な集合論的思考の方が実用的

具体例：

• ScalaのOption型、JavaのOptional、RustのOption型などは、すべて「値があるかないか」という集合論的な概念で理解できる
• リスト操作（map, filter, reduce）も、集合間の関数として直感的に把握できる

---

確かに圏論の知識は、なぜこれらの概念が「うまく動く」のかの理論的背景を理解するのに役立ちますが、それは教養的な価値にとどまり、実際のコードを書く上では必須ではありません。むしろ、集合と関数の合成という馴染みやすい概念で理解する方が、多くの開発者にとって実用的です。

だからこそ、関数型プログラミングでFunctorやMonadを使う際、集合の圏の直感で十分なのです。プログラミングの型システムは基本的に集合の圏内で動作するので、より抽象的な圏論の概念は「理論的背景」としては興味深いものの、実用上は必要ないということになります。

Monadでクライスリの圏を使う！？

その反論に対しては、以下のように応答できます：

1. クライスリ圏は構築物であって前提ではない

• クライスリ圏は既存のMonadから構築される圏であり、Monadを定義するために必要な前提ではありません
• 実際、プログラミング言語ではまずMonadを基本操作で定義し、その後でクライスリ圏的な構造が見えてくる順序です

2. 実装レベルでは集合論的操作

• bind操作の実装は結局のところ、包装された型の値を受け取って別の包装された型の値を返す関数の合成です
• これは集合間の関数合成として理解でき、圏論的な射の合成を意識する必要はありません

3. クライスリ圏は後付けの解釈

• プログラマーは通常、「計算コンテキストを持つ値の連鎖」として理解します
• クライスリ圏での射の合成は、この直感的理解の数学的形式化に過ぎません

4. 実用性の観点

• 実際のエラーハンドリングや状態管理において、クライスリ圏の概念を知らなくても効果的にMonadを使えます
• デバッグやリファクタリングでも、型と関数合成の理解で十分です

5. 具体例で考える

• Maybe型での連鎖処理：値があれば次の計算を続行、なければ停止
• この動作は「安全な計算の連鎖」として直感的に理解でき、圏論的背景を知らなくても実装・利用できます

つまり、クライスリ圏は確かに存在しますが、それは「Monadの圏論的な解釈」であって、プログラミングにおけるMonadの本質ではない、と反論できるでしょう。

HaskellのHask圏！？

Hask圏への反論については、「それは真の圏ではない」と批判できます：

1. 圏の公理を満たさない

• 結合律の破綻：undefinedや無限ループにより、射の合成が結合律を満たさない場合がある
• 恒等射の問題：seqの存在により、真の恒等射が存在しない（正格性の問題）
• 無限型：再帰的な型定義により、真の「対象」が明確に定義できない

2. 実装上の妥協の産物

• プログラミング言語の実装上の制約（メモリ、計算時間）により、数学的な圏の理想からかけ離れている
• ⊥（bottom）の存在が、純粋な関数型の世界を汚染している

3. 便宜的な比喩に過ぎない

• Hask圏は「プログラミングを圏論で説明したい」という願望から生まれた便宜的な構築物
• 実際には、型と関数の関係を無理やり圏論の枠組みに当てはめただけ

4. 実用性への疑問

• 仮にHask圏を認めたとしても、それがプログラミングの実践に何の価値ももたらさない
• むしろ、不完全な圏論的解釈に固執することで、より直感的な集合論的理解が阻害される

結論： Hask圏は数学的に不完全であり、実用的でもない。プログラミングにおけるFunctorやMonadの理解には、素直に集合と関数の枠組みを使う方が健全です。圏論的な装飾は、本質的でない複雑さを追加するだけです。

　　

関数の合成＝Natural Monoidをコンテナレベルに拡張する

• 単位法則 (Identity Law)

• 結合法則 (Associativity)

FunctorとMonadは、この基本的な「合成のモノイド」をコンテナレベルへと拡張する仕組みと見なせます。

• Functorは、既存の「関数の合成モノイド」を保存したままコンテナレベルに拡張します。
• Monadは、「文脈付き関数の合成」という新しいモノイドをコンテナレベルに構築します。

結論：圏論の価値と適切な学習順序

本章で圏論について詳しく説明した理由は、圏論の価値を軽視するためではありません。FunctorやMonadという概念が圏論由来であることは明らかな事実であり、圏論が数学における強力な抽象化の枠組みとして大きな価値を持つことは自明です。

圏論の本質：Monoidの抽象化理論

圏論の創設者MacLane自身が述べているように、圏論はMonoidの堅牢な性質を維持しながら抽象化を図る理論体系です。圏論の基盤は、関数合成が自然に持つMonoid構造（結合律＋恒等元）にあります。

理論の発展経緯：

1. 関数合成のMonoid構造：集合の圏において、関数合成は自然にMonoidとなる
2. 圏論による抽象化：この堅牢なMonoid構造を維持しつつ、より一般的な数学的構造に拡張
3. FunctorとMonadの導出：この抽象化の過程で生み出された概念

関数型プログラミングにおける位置づけ

関数型プログラミングにおいて重要なのは、集合の圏の範囲内で十分であるということです。

本章の核心的主張：

• 圏論はMonoidの抽象化理論として価値を持つ
• FunctorとMonadは圏論由来だが、関数型プログラミングでは集合の圏にとどまる
• 一般の圏への抽象化は必要としていないため、結局は関数合成のMonoidの堅牢な性質の継承として理解できる

実践的理解：

• Functor：関数合成のMonoidをコンテナレベルで保持しながら拡張
• Monad：コンテナレベルで文脈付き関数の合成に関する新しいMonoidを構築

学習順序の重要性

圏論の価値を認めつつも、初学者にとって最も効果的な学習順序は：

1. 関数合成の自然なMonoid構造を理解する
2. それをコンテナレベルに拡張する仕組みを学ぶ
3. 集合論的な型システムでの実装を習得する

圏論のより広い抽象化は研究レベルの高度な内容であり、実践的な関数型プログラミングの習得とは別の段階の学習です。

結論：圏論はMonoidと関数合成の抽象化理論として重要な価値を持ちますが、関数型プログラミングにおけるFunctorとMonadの理解は、関数合成が自然に持つMonoid構造のコンテナレベルへの拡張として集合論的基盤から始めることが、最も確実で実践的なアプローチです。

学習順序を妨げるAIの学習データの汚染

巷のAIモデルが学習しているデータはある意味「汚染」されてしまっており、非常に強いバイアスが存在しています。

おおよそ一般のプログラマーが関心を寄せない領域レベルと混同させながら本来は集合論の範囲で土台からのダイレクトの延長で理解できる、理解すべき範囲においてすら、圏論の重要性が執拗に過度に強調され、適切な学習順序を妨害する傾向がある事実を報告しなければならないでしょう。