Function Composition: A Natural Monoid

In the previous sections, we learned about the Monoid as an algebraic structure: a set (or Type) with an associative binary operation (a function of type 'a -> 'a -> 'a) and an identity element for that operation. Now, let’s explore a fascinating and highly relevant example: function composition itself, under specific conditions, forms a monoid.

Function Composition as a Binary Operation

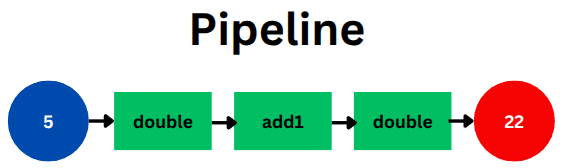
We often “concatenate” or “chain” functions in our data transformation pipelines. For example, if double is a function of type int -> int and add1 is also int -> int, we might write:

let composedFuncExample = double >> add1 >> double
// Creates a new function, also of type int -> int
// When applied to an input 'x',
// composedFuncExample behaves as x |> double |> add1 |> double

Here, >> is the function composition operator. In F#, f >> g creates a new function that first applies f to its input, and then applies g to the result of f. The general type signature for this operator is ('a -> 'b) -> ('b -> 'c) -> ('a -> 'c). It takes a function from 'a to 'b, and a function from 'b to 'c, and returns a new function from 'a to 'c.

For function composition to act as a binary operation that forms a monoid, we typically consider a specific set of functions: endofunctions on a type T. An endofunction is a function whose domain and codomain are the same type, i.e., functions of type T -> T.

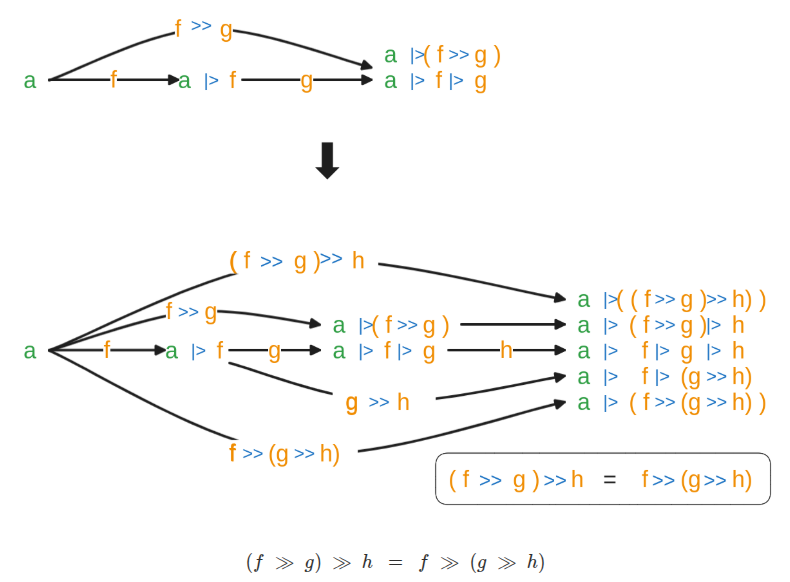
Let Fun(T,T) represent the set of all functions of type T -> T. The function composition operator >>, when applied to two functions from this set, acts as a binary operation that is closed within this set: >> : (T -> T) -> (T -> T) -> (T -> T) It takes two functions of type T -> T (e.g., f: T -> T and g: T -> T) and produces a new function f >> g, which is also of type T -> T.

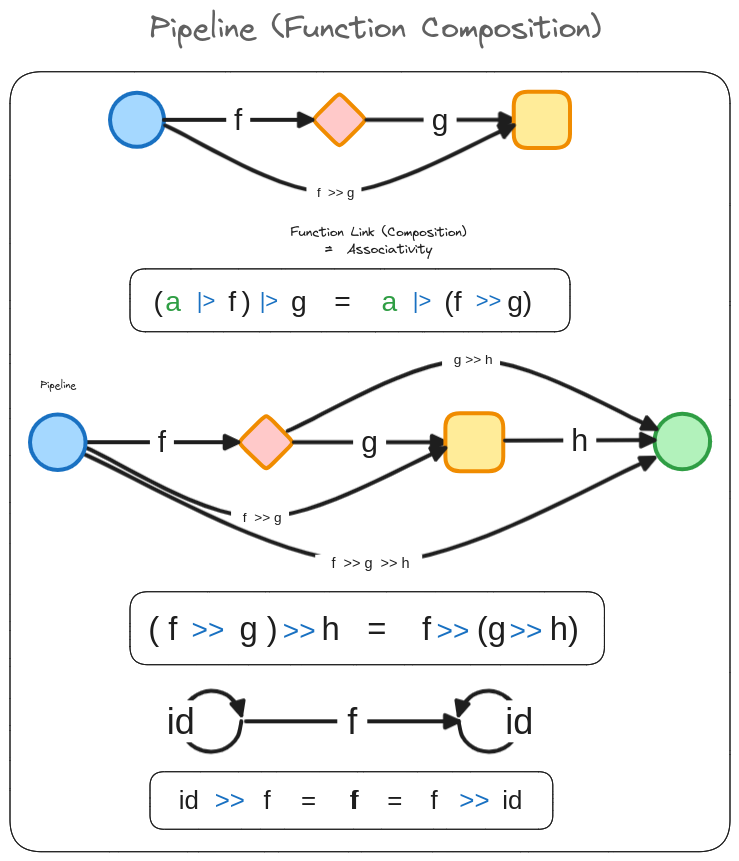
(This diagram visually represents f >> g, where if f: T -> T and g: T -> T, then their composition is also T -> T.)

Associativity of Function Composition (on T -> T functions)

This binary operation of function composition (>> on T -> T functions) is associative. For any three endofunctions f: T -> T, g: T -> T, and h: T -> T: (f >> g) >> h is functionally equivalent to f >> (g >> h).

Both expressions result in a single composite function that, when applied to an input x of type T, yields the same output. For example, let’s consider double: int -> int. The expression 1 |> double |> double can be understood in terms of function composition:

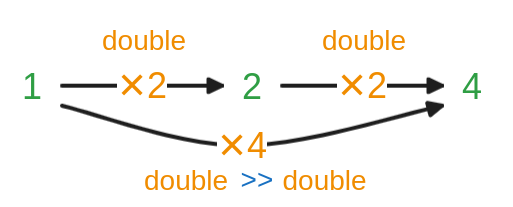
// Assuming 'double : int -> int'
// 1 |> double |> double evaluates to 4.
// This is equivalent to applying a composed function (double >> double) to 1:
// 1 |> (double >> double) also evaluates to 4.

The way double functions are grouped in composition doesn’t change the final outcome when applied to 1.

This principle extends to three or more functions. The following diagrams illustrate the associativity for f, g, and h (all T -> T): The composition (f >> g) >> h (first compose f and g, then compose the result with h):

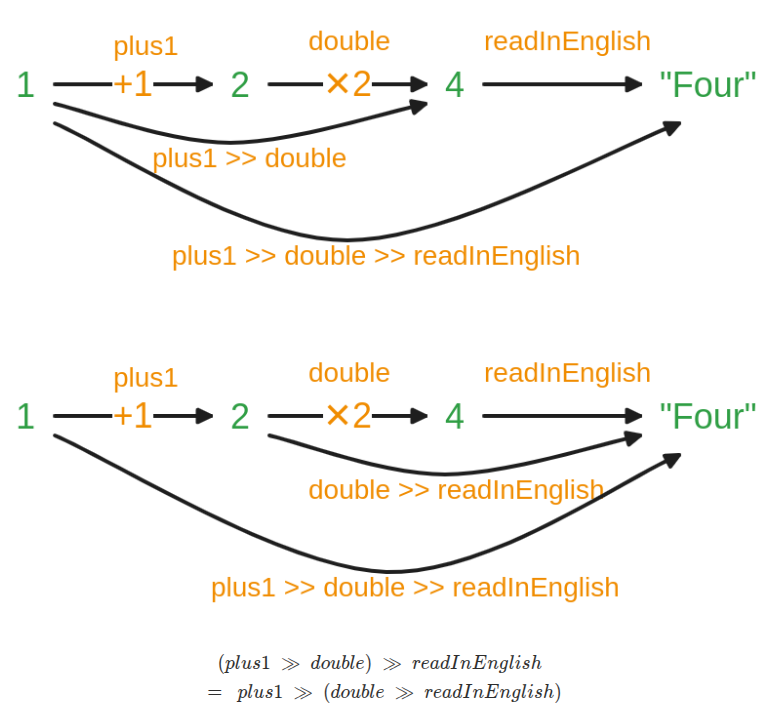
And the composition f >> (g >> h) (first compose g and h, then compose f with the result):

Applying either of these fully composed functions to an input value yields the exact same result. This associative property is fundamental.

The text below, and the subsequent diagram, explain that various operations, including function pipelines (which are built by applying composed functions), exhibit associativity. The “Function Pipeline is Associative” concept, in the context of applying a sequence of functions f, g, h to an input, means that the way these functions are composed into a single conceptual transformation doesn’t alter the final input-to-output mapping. The diagram below illustrates different ways to group the composition of f, g, and h within a pipeline structure, all leading to the same Output from a given Input.

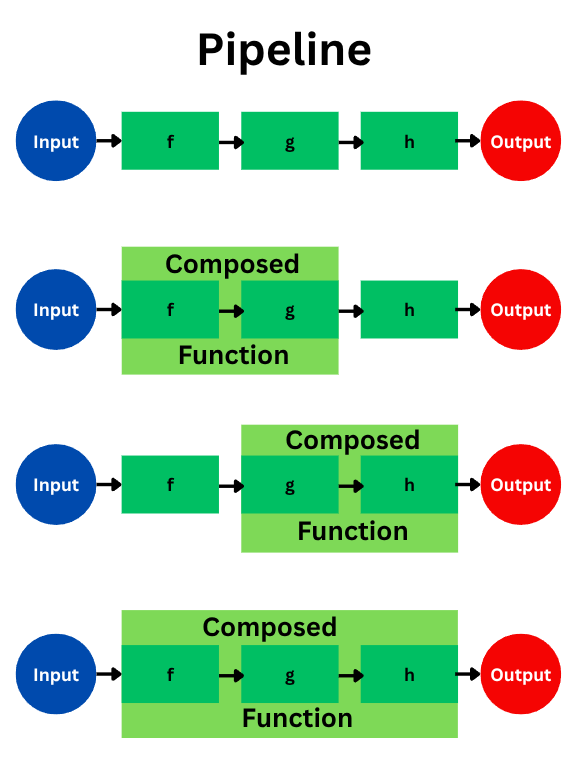When visualized, each of these compositional groupings represents the same overall transformation, differing only in the conceptual intermediate steps of how the composite function is built.

It’s important to distinguish the associativity of the function composition operator >> (which is about how new functions are built from other functions) from the associativity of the pipeline operator |> (which is left-associative, e.g., x |> f |> g is (x |> f) |> g, dictating the order of application). The associativity of >> ensures that the logical function created by f >> g >> h is unambiguous, regardless of whether we think of it as (f >> g) >> h or f >> (g >> h).

The Identity Function: The Identity Element for Composition

For the binary operation of function composition on the set of T -> T functions, the identity element is the identity function id: T -> T. As we recall from Unit 1, the identity function simply returns its input unchanged: id x = x.

(Here, 'a corresponds to our specific type T, so id is T -> T)

(If id is used in a context where T is int, its type is int -> int)

For any function f: T -> T:

• f >> id = f (right identity: composing f with id yields f)
• id >> f = f (left identity: composing id with f yields f) This holds because (f >> id) x means id (f x), which evaluates to f x. Similarly, (id >> f) x means f (id x), which also evaluates to f x.

Function Composition (of T -> T functions) Forms a Monoid

Given the above properties for the set of endofunctions on a type T:

1. Set: The set of all functions of type T -> T.
2. Binary Operation: Function composition >>, with type (T -> T) -> (T -> T) -> (T -> T).
3. Associativity: The >> operation is associative.
4. Identity Element: The identity function id: T -> T.

Therefore, (Set of functions T -> T, function composition >>, identity function id: T -> T) forms a Monoid.

(This diagram illustrates that the (Set of T->T functions, >> operator, id function) fits the Monoid structure, analogous to (Numbers, +, 0)).

This is a profound realization. The very act of composing functions—a cornerstone of functional programming and pipeline construction—shares the same robust algebraic structure (Monoid) as familiar operations like integer addition or string concatenation. This structural consistency is a key source of the elegance, predictability, and composability found in functional programming.

The algebraic laws are directly analogous:

• Integer Addition Monoid: (a + b) + c = a + (b + c) and 0 + a = a = a + 0
• Function Composition Monoid (on T->T): (f >> g) >> h = f >> (g >> h) and id >> f = f = f >> id

Understanding this allows us to leverage the properties of monoids when reasoning about and constructing complex sequences of function applications.